题目内容
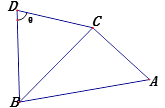
【题目】如图,在菱形ABCD中,∠ABC=60°,AC与BD相交于点O,AE⊥平面ABCD,CF//AE,AB=AE=2.
(1)求证:BD⊥平面ACFE;
(2)当直线FO与平面BDE所成的角为45°时,求二面角B﹣EF﹣D的余弦值.
【答案】
(1)证明:在菱形 ![]() 中,可得
中,可得 ![]() ,又因为
,又因为 ![]() 平面
平面 ![]() ,
, ![]() ,且
,且 ![]() 平面
平面 ![]()
(2)解:取 ![]() 的中点为
的中点为 ![]() ,以
,以 ![]() 为坐标原点,以
为坐标原点,以 ![]() 为
为 ![]() 轴,以
轴,以 ![]() 为
为 ![]() 轴,以
轴,以 ![]() 为
为 ![]() 轴,建立空间直角坐标系,则
轴,建立空间直角坐标系,则 ![]() ,则
,则 ![]() ,设平面
,设平面 ![]() 的法向量
的法向量 ![]() ,
,
由  ,也就是
,也就是 ![]() ,可取
,可取 ![]() ①
①
则 ![]() ,解得
,解得 ![]() ,故
,故 ![]()
![]()
设平面 ![]() 的法向量为
的法向量为 ![]()
设平面 ![]() 的法向量为
的法向量为 ![]() ,
,
同理①可得 ![]()
则 ![]() ,则二面角
,则二面角 ![]() 的余弦值为
的余弦值为 ![]()
【解析】本题主要考查空间二面角的求法以及线面垂直的判定定理的应用。(1)主要是利用线面垂直的判定定理和性质定理进行证明。(2)建立空间直角坐标系,利用向量坐标进行求解。
【考点精析】关于本题考查的直线与平面垂直的判定,需要了解一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能得出正确答案.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目