题目内容
已知f(x)=
x3+
(a+1)x2+(a+b+1)x+1，若方程f′（x）=0的两个实数根可以分别作为一个椭圆和双曲线的离心率，则（ ）
| 1 |
| 3 |
| 1 |
| 2 |
| A．a-b＜-3 | B．a-b≤-3 | C．a-b＞-3 | D．a-b≥-3 |
f′（x）=x2+（a+1）x+（a+b+1）
结合椭圆及双曲线的性质可得：f′（x）=x2+（a+1）x+（a+b+1）=0有一个大于1的根，一个小于1大于0作出不等式组
则
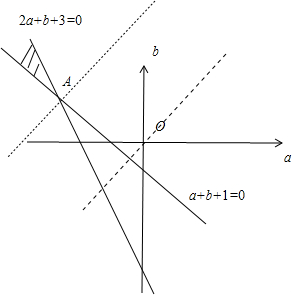
所表示的平面区域如图所示，令Z=a-b
作直线l0：a-b=0，把直线向可行域平移到A（-2，1）时，Zmax=-3
∴a-b＜-3
故选A．
结合椭圆及双曲线的性质可得：f′（x）=x2+（a+1）x+（a+b+1）=0有一个大于1的根，一个小于1大于0作出不等式组
则
|
所表示的平面区域如图所示，令Z=a-b
作直线l0：a-b=0，把直线向可行域平移到A（-2，1）时，Zmax=-3
∴a-b＜-3
故选A．
练习册系列答案
相关题目
时，求曲线
在点
处的切线方程；
时，讨论
的单调性.
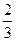x3-2ax2+3x(x∈R)． 
，若，
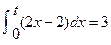,则
。