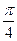题目内容
已知点P是抛物线y2＝4x上的动点，焦点是F，点A(3,2)，求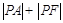
取得最小值时P点的坐标是（ ）．
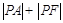取得最小值时P点的坐标是（ ）．| A．（1，―2） | B．（1，2） | C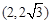． | D． |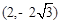
B
由P向准线x=-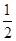
作垂线，垂足为M，由抛物线的定义，PF=PM，再由定点A向准线作垂线，垂足为N，那么点P在该抛物线上移动时，有PA+PF=PA+PM≥AN，当且仅当A，P，N三点共线时，
取得最小值AN=3-（-）=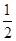
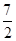，此时P的纵坐标为2，继而求得横坐标为1．
故|PA|+|PF|取得最小值时P点的坐标是（1，2），
故选B．
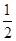作垂线，垂足为M，由抛物线的定义，PF=PM，再由定点A向准线作垂线，垂足为N，那么点P在该抛物线上移动时，有PA+PF=PA+PM≥AN，当且仅当A，P，N三点共线时，取得最小值AN=3-（-
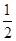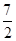）=，此时P的纵坐标为2，继而求得横坐标为1．故|PA|+|PF|取得最小值时P点的坐标是（1，2），
故选B．
练习册系列答案
口算能手系列答案
相关题目
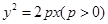上一点M(1,m) (m>0)到其焦点的距离为5,双曲线
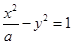的左顶点为A.若双曲线的一条渐近线与直线AM平行,则实数
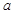等于 .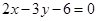
与坐标轴的交点为焦点的抛物线的标准方程为（ ）
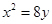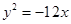
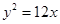
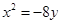或
或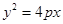
（p>0）的准线与x轴交于M点，过点M作直线l交抛物线于A、B两点.
+
+…+
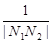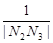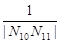的值.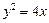
的焦点坐标是 ▲ ．
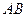为过抛物线
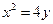焦点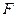
的一条弦，设
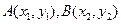，以下结论正确的是_______
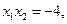且
； 
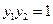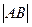的最小值为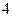
； 
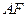为直径的圆与
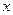轴相切；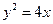 
上的两点A、B满足
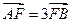,则弦AB的中点到准线的距离为____