题目内容
8.已知数列{an}满足a1=1,an+an+1=2n+1,n∈N*,Sn是数列{$\frac{1}{{a}_{n}}$}的前n项和,则下列结论:①S2n-1=(2n-1)•$\frac{1}{{a}_{n}}$;②S2n=$\frac{1}{2}$Sn;③S2n≥$\frac{3}{2}$-$\frac{1}{{2}^{n}}$+$\frac{1}{2}$Sn;④S2n≥Sn+$\frac{1}{2}$,其中正确的是③④(填写所有正确结论的序号).分析 易知,a2=2,由an+an+1=2n+1,an+1+an+2=2n+3,两式相减,得an+2-an=2,即此数列每隔一项成等差数列,可得an=n.
①令n=2,即可判断出正误;
②令n=1,即可判断出正误;
③作差${S_{2n}}-\frac{1}{2}{S_n}=1+\frac{1}{3}+\frac{1}{5}+…+\frac{1}{2n-1}$,利用$\frac{1}{2n-1}>\frac{1}{2^n}$,即可判断出正误;
④作差:${S_{2n}}-{S_n}=\frac{1}{n+1}+\frac{1}{n+2}+…\frac{1}{2n}$,设$f(n)=\frac{1}{n+1}+\frac{1}{n+2}+…+\frac{1}{2n}$,判断出其单调性,即可判断出正误.
解答 解:易知,a2=2,由an+an+1=2n+1,an+1+an+2=2n+3,
两式相减,得an+2-an=2,
即此数列每隔一项成等差数列,由a1=1,可得数列1的奇数项为1,3,5,…,
由a2=2,可得其偶数项为2,4,6,…,
故an=n.
①令n=2,${S_{2n-1}}={S_3}=\frac{11}{6}$,$({2n-1})•\frac{1}{a_n}=\frac{3}{2}$,${S_{2n-1}}≠({2n-1})•\frac{1}{a_n}$,①错;
②令n=1,${S_{2n}}={S_2}=1+\frac{1}{2}=\frac{3}{2}$,$\frac{1}{2}{S_n}=\frac{1}{2}{S_1}=\frac{1}{2}$,${S_{2n}}≠\frac{1}{2}{S_n}$,②错;
③∵${S_{2n}}-\frac{1}{2}{S_n}=1+\frac{1}{3}+\frac{1}{5}+…+\frac{1}{2n-1}$,又2n>2n-1,∴$\frac{1}{2n-1}>\frac{1}{2^n}$,
∴$1+\frac{1}{3}+\frac{1}{5}+…+\frac{1}{2n-1}≥1+\frac{1}{4}+\frac{1}{8}+…+\frac{1}{2^n}=\frac{3}{2}-\frac{1}{2^n}$,故③正确;
④∵${S_{2n}}-{S_n}=\frac{1}{n+1}+\frac{1}{n+2}+…\frac{1}{2n}$,设$f(n)=\frac{1}{n+1}+\frac{1}{n+2}+…+\frac{1}{2n}$,
∵$f({n+1})-f(n)=\frac{1}{2n+1}+\frac{1}{2n+2}-\frac{1}{n+1}=\frac{1}{2n+1}-\frac{1}{2n+2}>0$,
∴f(n+1)>f(n),∴f(n)单增,∴$f(n)≥f(1)=\frac{1}{2}$,∴${S_{2n}}-{S_n}≥\frac{1}{2}$,
∴${S_{2n}}≥{S_n}+\frac{1}{2}$(n∈N*),故④正确.
综上可得:只有③④正确.
故答案为:③④.
点评 本题考查了递推式的应用、等差数列的通项公式及其前n项和公式、数列的单调性,考查了“作差法”、推理能力与计算能力,属于中档题.

| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{\sqrt{7}}{4}$ |
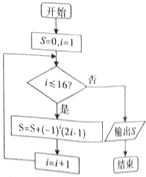
| A. | 14 | B. | 16 | C. | 19 | D. | 21 |
| A. | (1,2) | B. | ($\sqrt{2}$,$\sqrt{3}$) | C. | ($\sqrt{3}$,2) | D. | ($\sqrt{2}$,2) |