题目内容
【题目】如图，在四棱锥P﹣ABCD中，底面ABCD是菱形，且∠DAB=60°．点E是棱PC的中点，平面ABE与棱PD交于点F． （Ⅰ）求证：AB∥EF；
（Ⅱ）若PA=PD=AD，且平面PAD⊥平面ABCD，求平面PAF与平面AFE所成的锐二面角的余弦值．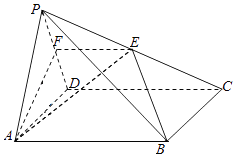
【答案】证明：（Ⅰ）因为底面ABCD是菱形，所以AB∥CD． 又因为AB面PCD，CD面PCD，所以AB∥面PCD．
又因为A，B，E，F四点共面，且平面ABEF∩平面PCD=EF，
所以AB∥EF．
解：（Ⅱ）取AD中点G，连接PG，GB．
因为PA=PD，所以PG⊥AD．
又因为平面PAD⊥平面ABCD，
且平面PAD∩平面ABCD=AD，
所以PG⊥平面ABCD．所以PG⊥GB．
在菱形ABCD中，因为AB=AD，∠DAB=60°，G是AD中点，
所以AD⊥GB．
如图，以G为原点，GA为x轴，GB为y轴，GP为z轴，建立空间直角坐标系G﹣xyz．
设PA=PD=AD=2a，
则G（0，0，0），A（a，0，0）， 
．
又因为AB∥EF，点E是棱PC中点，所以点F是棱PD中点．
所以 
．
所以 
．
设平面AFE的法向量为n=（x，y，z），则有 
所以 
令x=3，则平面AFE的一个法向量为 
．
因为BG⊥平面PAD，所以 
是平面PAF的一个法向量．
因为 
，
所以平面PAF与平面AFE所成的锐二面角的余弦值为 
． 
【解析】（Ⅰ）推导出AB∥CD，从而AB∥面PCD，由此能证明AB∥EF． （Ⅱ）取AD中点G，连接PG，GB．以G为原点，GA为x轴，GB为y轴，GP为z轴，建立空间直角坐标系G﹣xyz．利用向量法能求出平面PAF与平面AFE所成的锐二面角的余弦值．
【考点精析】本题主要考查了空间中直线与直线之间的位置关系的相关知识点，需要掌握相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；异面直线： 不同在任何一个平面内，没有公共点才能正确解答此题．
