题目内容
【题目】已知在平面直角坐标系
中，直线
（
为参数），以原点为极点，
轴的非负半轴为极轴且取相同的单位长度建立极坐标系，曲线
的极坐标方程为
.
（1）求直线
的普通方程及曲线的直角坐标方程；
（2）设点
直角坐标为
，直线与曲线交于
，
两点，求
的值.
【答案】（1）直线
的普通方程为
，曲线
的直角坐标方程为
；（2）3.
【解析】
（1）由参数方程消去参数即可得到普通方程，由极坐标方程与直角坐标方程的互化即可得出直角坐标方程；
（2）先将直线的参数方程化为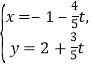
（
为参数），代入曲线C的方程，根据参数的几何意义即可求出结果.
解：（1）直线的普通方程为
.
因为
，
所以
，
所以
.
故曲线的直角坐标方程为
.
（2）据题设分析知，直线的参数方程为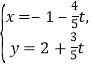（为参数）.
代直线的参数方程入曲线的方程并化简，得
.
由参数的几何意义知，
.
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
【题目】随着5G商用进程的不断加快，手机厂商之间围绕5G用户的争夺越来越激烈，5G手机也频频降低身价飞人寻常百姓家．某科技公司为了给自己新推出的5G手机定价，随机抽取了100人进行调查，对其在下一次更换5G手机时，能接受的价格（单位：元）进行了统计，得到结果如下表，已知这100个人能接受的价格都在
之间，并且能接受的价格的平均值为2350元（同一组的数据用该组区间的中点值代替）．
分组 | 一 | 二 | 三 | 四 | 五 |
手机价格X（元） |
|
|
|
|
|
频数 | 10 | x | y | 20 | 20 |
（1）现用分层抽样的方法从第一、二、三组中随机抽取6人，将该样本看成一个总体，从中随机抽取2人，求其中恰有1人能接受的价格不低于2000元的概率；
（2）若人们对5G手机能接受的价格X近似服从正态分布
，其中
为样本平均数
，
为样本方差
，求
．
附：
．若
，则
，
．
