题目内容
1.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,|$\overrightarrow{a}$|=$\sqrt{2}$,$\overrightarrow{OA}$=$\overrightarrow{a}$-$\overrightarrow{b}$,$\overrightarrow{OB}$=$\overrightarrow{a}$+$\overrightarrow{b}$,若△AOB是以O为直角顶点的等腰直角三角形,则△AOB的面积为( )| A. | 8 | B. | 4 | C. | 2 | D. | 1 |
分析 根据题意,画出图形,结合图形,利用平面向量的数量积求出模长,即可计算△ABC的面积.
解答 解:根据题意,画出图形,如图所示,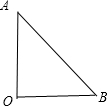
∵$\overrightarrow{OA}$⊥$\overrightarrow{OB}$,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|,
∴$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,
即($\overrightarrow{a}$-$\overrightarrow{b}$)($\overrightarrow{a}$+$\overrightarrow{b}$)=0,
∴|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=$\sqrt{2}$,
由|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|得,
|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$|,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=0,
∴|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{{|\overrightarrow{a}|}^{2}{+|\overrightarrow{b}|}^{2}}$=2;
∴S△AOB=$\frac{1}{2}$×2×2=2.
故选:C.
点评 本题考查了平面向量数量积的应用问题,也考查了求三角形的面积问题,是基础题目.

| A. | 1 | B. | -1 | C. | $\sqrt{2}$ | D. | $-\sqrt{2}$ |
| A. | 若a>b,则ac2>bc2 | B. | 若a>b,则a2>b2 | ||
| C. | 若a>b,c>d,则a-c>b-d | D. | 若a<b<0,则$\frac{1}{a}$>$\frac{1}{b}$ |
| x | 0 | 1 | 2 | 3 |
| y | -1 | 1 | m | 8 |
| A. | 4 | B. | $\frac{9}{2}$ | C. | 5 | D. | 6 |