题目内容
【题目】已知圆O:x2+y2=2,直线l:y=kx﹣2.
(1)若直线l与圆O交于不同的两点A,B,且 ![]() ,求k的值;
,求k的值;
(2)若 ![]() ,P是直线l上的动点,过P作圆O的两条切线PC,PD,切点分别为C,D,求证:直线CD过定点,并求出该定点的坐标.
,P是直线l上的动点,过P作圆O的两条切线PC,PD,切点分别为C,D,求证:直线CD过定点,并求出该定点的坐标.
【答案】
(1)解:因为 ![]() ,所以原点O到直线l的距离为
,所以原点O到直线l的距离为 ![]() ,
,
又因为 ![]() ,
,
所以 ![]() .
.
(2)证明:由题意可知O,P,C,D四点共圆,且在以OP为直径的圆上,
设 ![]() ,
,
则以OP为直径的圆的方程为: ![]() ,
,
即 ![]() ,
,
又C,D在圆O:x2+y2=2上,
所以直线CD的方程为 ![]() ,
,
即 ![]() .
.
因为t∈R,所以 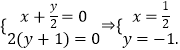
所以直线CD过定点 ![]() .
.
【解析】(1)由 ![]() ,得到原点O到直线l的距离为1,由此利用点到直线的距离公式能求出k的值.(2)由题意可知O,P,C,D四点共圆,且在以OP为直径的圆上,设
,得到原点O到直线l的距离为1,由此利用点到直线的距离公式能求出k的值.(2)由题意可知O,P,C,D四点共圆,且在以OP为直径的圆上,设 ![]() ,以OP为直径的圆的方程为
,以OP为直径的圆的方程为 ![]() ,由C,D在圆O:x2+y2=2上,求出直线CD的方程,由此能证明直线CD过定点
,由C,D在圆O:x2+y2=2上,求出直线CD的方程,由此能证明直线CD过定点 ![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


