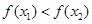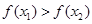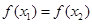题目内容
|
已知 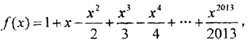 设函数F(x)= f(x+4),且F(x)的零点均在区间[a,b](a<b,a,b 设函数F(x)= f(x+4),且F(x)的零点均在区间[a,b](a<b,a,b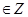 ) 内,,则x2+y2=b-a的面积的最小值为( ) ) 内,,则x2+y2=b-a的面积的最小值为( )
|
A
试题分析:验证
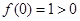 ,
,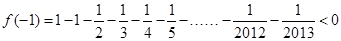
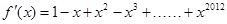
易知
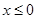 时,
时,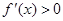 ;
;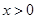 时,
时,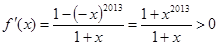
所以
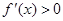 在
在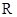 上恒成立,故
上恒成立,故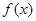 在
在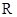 上是增函数,又
上是增函数,又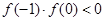 ,
,∴
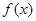 只有一个零点,记为
只有一个零点,记为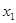 ,则
,则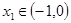 .
.故
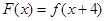 的零点
的零点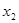 即将
即将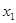 向左平移
向左平移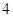 个单位,
个单位, 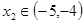 ,
,又函数
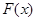 的零点均在区间
的零点均在区间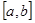 内,且
内,且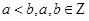 ,故当
,故当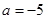 ,
,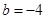
时,即
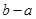 的最小值为
的最小值为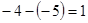 ,即圆
,即圆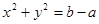 的半径取得最小值
的半径取得最小值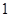 ,所以面积取得最小值
,所以面积取得最小值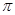 ,故选
,故选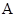

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,
,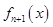 是
是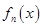 的导函数,即
的导函数,即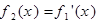 ,
,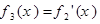 ,…,
,…,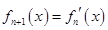 ,
,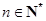 ,则
,则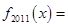 ( )
( )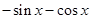
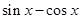
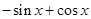
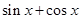
 ,
, .
. ,使得
,使得 ,求a的取值范围;
,求a的取值范围; 有两个不同的实数解
有两个不同的实数解 ,证明:
,证明: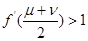 .
.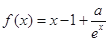 (
(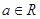 ,
,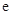 为自然对数的底数).
为自然对数的底数).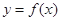 在点
在点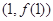 处的切线平行于
处的切线平行于 轴,求
轴,求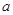 的值;
的值;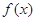 的极值;
的极值;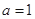 的值时,若直线
的值时,若直线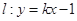 与曲线
与曲线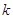 的最大值.
的最大值.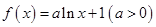 .
.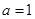 且
且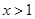 时,证明:
时,证明: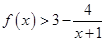 ;
;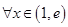 ,
,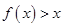 恒成立,求实数
恒成立,求实数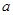 的取值范围;
的取值范围;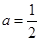 时,证明:
时,证明: .
.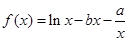 (
(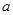 、
、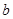 为常数),在
为常数),在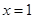 时取得极值.
时取得极值.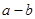 的值;
的值;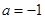 时,求函数
时,求函数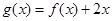 的最小值;
的最小值;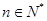 时,试比较
时,试比较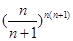 与
与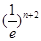 的大小并证明.
的大小并证明.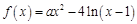 ,
,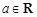 .
.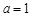 时,求
时,求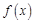 的单调区间;
的单调区间;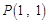 和函数
和函数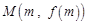 ,对任意
,对任意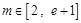 ,直线
,直线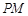 倾斜角都是钝角,求
倾斜角都是钝角,求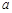 的取值范围.
的取值范围.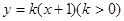 与函数
与函数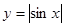 的图象恰有四个公共点
的图象恰有四个公共点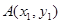 ,
,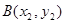 ,
,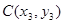 ,
,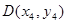 其中
其中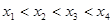 ,则有( )
,则有( )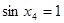
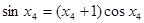
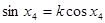
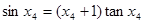
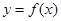 ,满足
,满足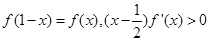 ,若
,若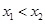 且
且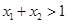 ,则有( )
,则有( )