题目内容
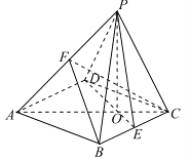
【题目】如图,已知四棱锥![]() 的底面是边长为
的底面是边长为![]() 的菱形,
的菱形,![]() ,点
,点![]() 是棱
是棱![]() 的中点,
的中点,![]() ,点
,点![]() 在平面
在平面![]() 的射影为
的射影为![]() ,
,![]() 为棱
为棱![]() 上一点,
上一点,
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 为棱
为棱![]() 的中点,
的中点,![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值。
所成角的正弦值。
【答案】(Ⅰ)详见解析(Ⅱ)![]()
【解析】
(Ⅰ)推导出BC⊥PO,BC⊥DE,从而BC⊥平面PED,由此能证明平面PED⊥平面BCF.
(Ⅱ)设AC∩BD=Q,以Q为原点,QB,QC分别为x,y轴,建立空间直角坐标系,利用向量法能求出直线CF与平面PAB所成角的正弦值.
(Ⅰ)![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]()
依题意得![]() 为等边三角形,
为等边三角形,![]() 为棱
为棱![]() 的中点,
的中点,![]()
又![]() 平面
平面![]() ,
,![]() 平面
平面![]()
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() .
.
(Ⅱ)设![]() ,以
,以![]() 为坐标原点,
为坐标原点,![]() 分别为
分别为![]() 轴,建立如图空间直角坐标系,
轴,建立如图空间直角坐标系,
则![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则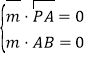 ,即
,即![]() ,令
,令![]() ,
,
得![]() ,
,
![]() ,故直线
,故直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]()

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
【题目】某工厂生产某种型号的农机具零配件,为了预测今年7月份该型号农机具零配件的市场需求量,以合理安排生产,工厂对本年度1月份至6月份该型号农机具零配件的销售量及销售单价进行了调查,销售单价![]() (单位:元)和销售量
(单位:元)和销售量![]() (单位:千件)之间的6组数据如下表所示:
(单位:千件)之间的6组数据如下表所示:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售单价 | 11.1 | 9.1 | 9.4 | 10.2 | 8.8 | 11.4 |
销售量 | 2.5 | 3.1 | 3 | 2.8 | 3.2 | 2.4 |
(1)根据1至6月份的数据,求![]() 关于
关于![]() 的线性回归方程(系数精确到0.01);
的线性回归方程(系数精确到0.01);
(2)结合(1)中的线性回归方程,假设该型号农机具零配件的生产成本为每件3元,那么工厂如何制定7月份的销售单价,才能使该月利润达到最大?(计算结果精确到0.1)
参考公式:回归直线方程![]() ,
,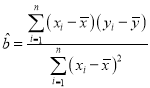
参考数据:![]() ,
,![]()
