题目内容
【题目】已知数列{an}满足a1=1，an+1=2an+n﹣1
（1）求证：数列{an+n}是等比数列；
（2）求数列{an}的通项和前n项和Sn ．
【答案】
（1）证明：由数列{an}满足a1=1，an+1=2an+n﹣1，变形为an+1+（n+1）=2（an+n）．
∴数列{an+n}是等比数列，其中首项为a1+1=2，公比为2；
（2）解：由（1）可得： 
，∴ 
．
∴Sn= 
=2n+1﹣2﹣ 
【解析】（1）由数列{an}满足a1=1，an+1=2an+n﹣1，变形为an+1+（n+1）=2（an+n）即可证明；（2）利用等比数列的通项公式、等比数列与等差数列的前n项和公式即可得出．
【考点精析】解答此题的关键在于理解等比关系的确定的相关知识，掌握等比数列可以通过定义法、中项法、通项公式法、前n项和法进行判断，以及对数列的前n项和的理解，了解数列{an}的前n项和sn与通项an的关系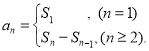
．
考前必练系列答案【题目】设关于某产品的明星代言费x（百万元）和其销售额y（百万元），有如表的统计表格：
i | 1 | 2 | 3 | 4 | 5 | 合计 |
xi（百万元） | 1.26 | 1.44 | 1.59 | 1.71 | 1.82 | 7.82 |
wi（百万元） | 2.00 | 2.99 | 4.02 | 5.00 | 6.03 | 20.04 |
yi（百万元） | 3.20 | 4.80 | 6.50 | 7.50 | 8.00 | 30.00 |
| ||||||
其中 
．
（1）在坐标系中，作出销售额y关于广告费x的回归方程的散点图，根据散点图指出：y=a+blnx，y=c+dx3哪一个适合作销售额y关于明星代言费x的回归类方程（不需要说明理由）； 
（2）已知这种产品的纯收益z（百万元）与x，y有如下关系：x=0.2y﹣0.726x（x∈[1.00，2.00]），试写出z=f（x）的函数关系式，试估计当x取何值时，纯收益z取最大值？（以上计算过程中的数据统一保留到小数点第2位）
