题目内容
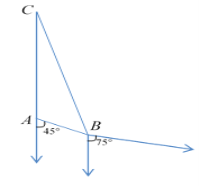
【题目】如图，在海岸A处，发现南偏东45°方向距A为(2
－2)海里的B处有一艘走私船，在A处正北方向，距A为
海里的C处的缉私船立即奉命以10海里/时的速度追截走私船．
（1）刚发现走私船时，求两船的距离；
（2）若走私船正以10
海里/时的速度从B处向南偏东75°方向逃窜，问缉私船沿什么方向能最快追上走私船？并求出所需要的时间(精确到分钟，参考数据：≈1.4，
≈2.5)．
【答案】（1）4海里；（2）缉私船沿南偏东60°方向，需47分钟才能追上走私船．
【解析】
⑴在
中，利用已知条件根据余弦定理求出
⑵根据正弦定理，求得
，再运用正弦定理求出结果
（1）在中，
∵
(2
－2)海里，
海里，
，
由余弦定理，得
(海里)．
（2）根据正弦定理，可得
，易知
，
设缉私船应沿CD方向行驶t小时，才能最快截获(在D点)走私船，
则有
海里)，
(海里)．而
，
在
中，根据正弦定理，可得
根据正弦定理，得
，解得
小时
分钟
故缉私船沿南偏东60°方向，需47分钟才能追上走私船．
练习册系列答案
天天练口算系列答案
相关题目
