题目内容
18.向量$\overrightarrow{a}$与向量$\overrightarrow{b}$($\overrightarrow{a}•\overrightarrow{c}$)-$\overrightarrow{c}$($\overrightarrow{a}•\overrightarrow{b}$)的数量积等于0.分析 直接利用向量的数量积求解即可.
解答 解:向量$\overrightarrow{a}$与向量$\overrightarrow{b}$($\overrightarrow{a}•\overrightarrow{c}$)-$\overrightarrow{c}$($\overrightarrow{a}•\overrightarrow{b}$)的数量积:$\overrightarrow{a}$•[$\overrightarrow{b}$($\overrightarrow{a}•\overrightarrow{c}$)-$\overrightarrow{c}$($\overrightarrow{a}•\overrightarrow{b}$)]=$\overrightarrow{a}•$$\overrightarrow{b}$($\overrightarrow{a}•\overrightarrow{c}$)-$\overrightarrow{a}•$$\overrightarrow{c}$($\overrightarrow{a}•\overrightarrow{b}$)
=0.
故答案为:0.
点评 本题考查向量的数量积的求法,考查计算能力.

练习册系列答案
相关题目
9.已知f(x)是R上的增函数,若a+b≥0,则有( )
| A. | f(a)+f(b)>f(-a)+f(-b) | B. | f(a)+f(b)≥f(-a)+f(-b) | C. | f(a)+f(b)<f(-a)+f(-b) | D. | f(a)+f(b)≤f(-a)+f(-b) |
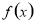 的定义域为
的定义域为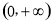 ,则函数
,则函数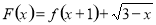 的定义域为( )
的定义域为( )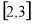 B.
B. 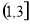 C.
C. 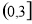 D.
D.