题目内容
7.已知x,y∈R,x2+y2≤10,求x-y的取值范围.分析 根据已知条件,写出圆的参数方程x=$\sqrt{10}$cosα,y=$\sqrt{10}$sinα,然后,结合辅助角公式进行求解其范围即可.
解答 解:∵x2+y2≤10,
∴可设x=$\sqrt{10}$cosα,y=$\sqrt{10}$sinα,
∴x-y=$\sqrt{10}$(cosα-sinα)
=$\sqrt{10}$cos(α+$\frac{π}{4}$)
∴x-y有最大值为$\sqrt{10}$,最小值为-$\sqrt{10}$,
∴x-y的取值范围[-$\sqrt{10}$,$\sqrt{10}$].
点评 本题重点考查了圆的参数方程、辅助角公式等知识,属于中档题,准确把握圆的参数方程是解题关键.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
12.函数f(x)=$\frac{2x+1}{x-1}$的单调递减区间是( )
| A. | (-∞,1)∪(1,+∞) | B. | (-∞,0)∪(0,+∞) | C. | (-∞,0),(0,+∞) | D. | (-∞,1),(1,+∞) |
 如图,二次函数y=-mx2+4m的顶点坐标为(0,2),矩形ABCD的顶点B、C在x轴上,A、D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内.
如图,二次函数y=-mx2+4m的顶点坐标为(0,2),矩形ABCD的顶点B、C在x轴上,A、D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内.
 的值
的值 ,b=2,求△ABC的面积S.
,b=2,求△ABC的面积S. 的图象上各点的横坐标伸长到原来的3倍,再向右平移
的图象上各点的横坐标伸长到原来的3倍,再向右平移 个单位,得到的函数的一个对称中心是 ( )
个单位,得到的函数的一个对称中心是 ( ) B.
B. 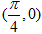 C.
C.  D.
D. 
 B,则实数a的取值范围是
B,则实数a的取值范围是