题目内容
1.已知抛物线C1:y2=2x的焦点F是双曲线C2:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的一个顶点,两条曲线的一个交点为M,若|MF|=$\frac{3}{2}$,则双曲线C2的离心率是( )| A. | $\sqrt{2}$ | B. | $\frac{{\sqrt{17}}}{3}$ | C. | $\frac{{2\sqrt{6}}}{3}$ | D. | $\frac{{\sqrt{33}}}{3}$ |
分析 通过题意可知F($\frac{1}{2}$,0)、不妨记M(1,$\sqrt{2}$),将点M、F代入双曲线方程,计算即得结论.
解答 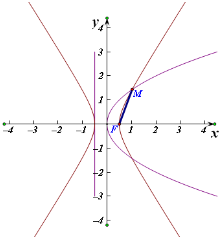 解:由题意可知F($\frac{1}{2}$,0),
解:由题意可知F($\frac{1}{2}$,0),
由抛物线的定义可知:xM=$\frac{3}{2}$-$\frac{1}{2}$=1,
∴yM=±$\sqrt{2}$,不妨记M(1,$\sqrt{2}$),
∵F($\frac{1}{2}$,0)是双曲线的一个顶点,
∴$\frac{\frac{1}{4}}{{a}^{2}}=1$,即a2=$\frac{1}{4}$,
又点M在双曲线上,∴$\frac{1}{\frac{1}{4}}-\frac{2}{{b}^{2}}=1$,即b2=$\frac{2}{3}$,
∴e=$\frac{c}{a}$=$\frac{\sqrt{{a}^{2}+{b}^{2}}}{a}$=$\frac{\sqrt{33}}{3}$,
故选:D.
点评 本题考查求双曲线的离心率,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
11.若定义在R上的函数满足f(-x)=f(x),f(4-x)=f(x),且当x∈[0,2]时,f(x)=$\sqrt{4-{x^2}}$,则函数H(x)=|xex|-f(x)在区间[-6,2]上的零点个数为( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
9.已知双曲线C1:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F也是抛物线C2:y2=2px(p>0)的焦点,C1与C2的一个交点为P,若PF⊥x轴,则双曲线C1的离心率为( )
| A. | $\sqrt{2}$+1 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{2}$-1 | D. | $\sqrt{3}$+1 |
16.二次函数y=kx2(x>0)的图象在点(an,an2)处的切线与x轴交点的横坐标为an+1,n为正整数,a1=$\frac{1}{3}$,若数列{an}的前n项和为Sn,则S5=( )
| A. | $\frac{3}{2}[{1-{{({\frac{1}{3}})}^5}}]$ | B. | $\frac{1}{3}[{1-{{({\frac{1}{3}})}^5}}]$ | C. | $\frac{2}{3}[{1-{{({\frac{1}{2}})}^5}}]$ | D. | $\frac{3}{2}[{1-{{({\frac{1}{2}})}^5}}]$ |
10.已知双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{6}$=1与抛物线y2=2px有公共焦点F,双曲线与抛物线的准线交于M、N两点,且△MNF为等边三角形,则p的值为( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4$\sqrt{2}$ | D. | 6 |
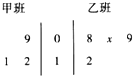 如图,茎叶图记录了某校甲班3名同学在一学年中去社会实践基地A实践的次数和乙班4名同学在同一学年中去社会实践基地B实践的次数.乙班记录中有一个数据模糊,无法确认,在图中用x表示.
如图,茎叶图记录了某校甲班3名同学在一学年中去社会实践基地A实践的次数和乙班4名同学在同一学年中去社会实践基地B实践的次数.乙班记录中有一个数据模糊,无法确认,在图中用x表示.