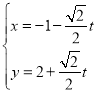题目内容
【题目】已知![]() ,数列
,数列![]() 中的每一项均在集合
中的每一项均在集合![]() 中,且任意两项不相等,又对于任意的整数
中,且任意两项不相等,又对于任意的整数![]() ,均有
,均有![]() .例如
.例如![]() 时,数列
时,数列![]() 为
为![]() 或
或![]() .
.
(1)当![]() 时,试求满足条件的数列
时,试求满足条件的数列![]() 的个数;
的个数;
(2)当![]() ,求所有满足条件的数列
,求所有满足条件的数列![]() 的个数.
的个数.
【答案】(1)4;(2)![]() .
.
【解析】
(1)分别假设![]() ,
,![]() 和
和![]() ,根据已知关系式可求得
,根据已知关系式可求得![]() ,从而得到结果;
,从而得到结果;
(2)①当![]() 时,可确定满足条件的数列只有
时,可确定满足条件的数列只有![]() 个;②当
个;②当![]() 时,可知
时,可知![]() 以后的各项是唯一确定的,根据
以后的各项是唯一确定的,根据![]() 之前的满足条件的数列的个数为
之前的满足条件的数列的个数为![]() 可整理得到
可整理得到![]() ,由等比数列通项公式可求得
,由等比数列通项公式可求得![]() ,由此可确定结果.
,由此可确定结果.
(1)若![]() ,则
,则![]() ,故
,故![]() ,则
,则![]() ;
;
若![]() ,则
,则![]() ,
,![]() ,故
,故![]() ,则
,则![]() ;
;
若![]() ,则
,则![]() ,
,![]() 或
或![]() ,
,![]() ;
;
![]() 当
当![]() 时,满足条件的数列
时,满足条件的数列![]() 为
为![]() ;
;![]() ;
;![]() ;
;![]() ;
;
故满足条件的![]() 的个数为
的个数为![]() ;
;
(2)设满足条件的数列![]() 的个数为
的个数为![]() ,显然
,显然![]() ,
,![]() ,
,![]() ,
,
不等式![]() 中取
中取![]() ,则有
,则有![]() ,即
,即![]() ,
,
①当![]() 时,则
时,则![]() ,同理
,同理![]() ,...,
,...,![]() ,满足条件的数列只有
,满足条件的数列只有![]() 个;
个;
②当![]() ,则
,则![]() ,同理
,同理![]() ,...,
,...,![]() ,即
,即![]() 以后的各项是唯一确定的,又
以后的各项是唯一确定的,又![]() 之前的满足条件的数列的个数为
之前的满足条件的数列的个数为![]() ,
,
![]() 当
当![]() 时,
时,![]() (*),
(*),
当![]() 时,
时,![]() ,代入(*)式得到
,代入(*)式得到![]() ,且满足
,且满足![]() ,
,
![]() 对任意
对任意![]() ,都有
,都有![]() 成立,又
成立,又![]() ,
,![]() ;
;
综上,满足条件的数列![]() 的个数为
的个数为![]() .
.

练习册系列答案
相关题目
【题目】A、B两种品牌各三种车型2017年7月的销量环比(与2017年6月比较)增长率如下表:
A品牌车型 | A1 | A2 | A3 | ||||
环比增长率 | -7.29% | 10.47% | 14.70% | ||||
B品牌车型 | B1 | B2 | B3 | ||||
环比增长率 | -8.49% | -28.06% | 13.25% | ||||
根据此表中的数据,有如下关于7月份销量的四个结论:①A1车型销量比B1车型销量多;
②A品牌三种车型总销量环比增长率可能大于14.70%;
③B品牌三款车型总销量环比增长率可能为正;
④A品牌三种车型总销量环比增长率可能小于B品牌三种车型总销量环比增长率.
其中正确结论的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()