题目内容
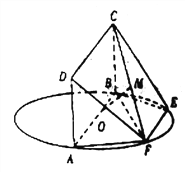
【题目】如图所示, ![]() 为圆
为圆![]() 的直径,点
的直径,点![]() ,
, ![]() 在圆
在圆![]() 上,
上, ![]() ,矩形
,矩形![]() 所在的平面和圆
所在的平面和圆![]() 所在的平面互相垂直,且
所在的平面互相垂直,且![]() ,
, ![]() ,
, ![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)设![]() 的中点为
的中点为![]() ,求三棱锥
,求三棱锥![]() 的体积
的体积![]() 与多面体
与多面体![]() 的体积
的体积![]() 之比的值.
之比的值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)证明![]() ,由圆的直径性质推出
,由圆的直径性质推出![]() ,然后证明
,然后证明![]() 平面
平面![]() ;(2)根据等级变换求三棱锥
;(2)根据等级变换求三棱锥![]() 的体积
的体积![]() ,多面体
,多面体![]() 的体积可分成三棱锥
的体积可分成三棱锥![]() 与四棱锥
与四棱锥![]() 的体积之和,可求出
的体积之和,可求出![]() ,进而可得比值.
,进而可得比值.
试题解析:(1)证明: ![]() 矩形
矩形![]() 所在的平面和平面
所在的平面和平面![]() 互相垂直,且
互相垂直,且![]() ,
,
![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
, ![]() .
.
又![]() 为圆
为圆![]() 的直径,
的直径,
![]() ,
,
又![]() ,
,
![]() 平面
平面![]() .
.
(2)设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,
则![]() ,
,
又![]() ,
, ![]() ,
,
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,
![]() ,
,
又![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
显然,四边形![]() 为等腰梯形,
为等腰梯形, ![]() ,因此
,因此![]() 为边长是1的正三角形.
为边长是1的正三角形.
三棱锥![]() 的体积
的体积![]()
![]()
![]()
多面体![]() 的体积可分成三棱锥
的体积可分成三棱锥![]() 与四棱锥
与四棱锥![]() 的体积之和,计算得两底间的距离
的体积之和,计算得两底间的距离![]() ,
,
![]()
![]()
![]() .
.
![]()
![]()
![]() .
.
![]()
![]() .
.
![]() .
.
【方法点晴】本题主要考查线面垂直、线线垂直及棱锥的体积公式,属于难题.证明直线和平面垂直的常用方法有:(1)利用判定定理;(2)利用判定定理的推论![]() ;(3)利用面面平行的性质
;(3)利用面面平行的性质![]() ;(4)利用面面垂直的性质,当两个平面垂直时,在一个平面内垂直于交线的直线垂直于另一个平面.
;(4)利用面面垂直的性质,当两个平面垂直时,在一个平面内垂直于交线的直线垂直于另一个平面.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目