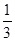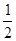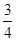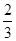题目内容
实系数方程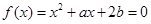
的一个根在（0，1）内，另一个根在（1，2）内，求：
（1）、
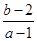的值域； （2）、
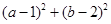的值域； （3）、
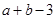的值域．
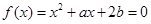的一个根在（0，1）内，另一个根在（1，2）内，求： （1）、
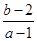的值域； （2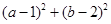）、的值域； （3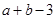）、的值域．（1）
（2）（8，17） （3）
．
（2）（8，17） （3）．本试题主要是考查了一元二次方程的根的分步问题的运用。
根据二次函数图像可知，实系数方程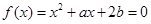的一个根在（0，1）内，另一个根在（1，2）内可知
进而得到可行域，在可行域内根据几何意义距离和线性目标函数得到相应的最值。
由题意：，画出可行域是由A（-3，1）、B（-2，0）、C（-1，0）所构成的三角形区域，利用各式的几何意义分别可得值域为：
（1） （2）（8，17） （3）．
根据二次函数图像可知，实系数方程
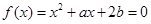的一个根在（0，1）内，另一个根在（1，2）内可知进而得到可行域，在可行域内根据几何意义距离和线性目标函数得到相应的最值。
由题意：
，画出可行域是由A（-3，1）、B（-2，0）、C（-1，0）所构成的三角形区域，利用各式的几何意义分别可得值域为：（1）
（2）（8，17） （3）．
练习册系列答案
名校课堂系列答案
相关题目
是二次函数，且满足
，
在
单调，求
的取值范围。
上是减函数，且
。
的值，并求出
和
的取值范围。
。
的取值范围，并写出当
的解析式。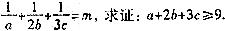
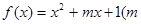为整数）且关于
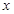的方程
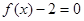在区间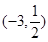
内有两个不同的实根，（1）求整数
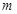的值；（2）若对一切
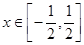，不等式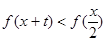
恒成立，求实数
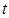的取值范围。
，
；
.
，那么广告效应D＝a
