题目内容
【题目】已知函数![]() 且
且![]() .
.
(Ⅰ)若函数![]() 在
在![]() 处取得极值,求实数
处取得极值,求实数![]() 的值.
的值.
(Ⅱ)若函数![]() 不存在零点,求实数
不存在零点,求实数![]() 的取值范围.
的取值范围.
【答案】(I)![]() ;
;
(II)![]()
【解析】
(Ⅰ)求函数的导数,利用函数![]() 在
在![]() 处取得极值,则
处取得极值,则![]() 即
即![]() ,再检验函数在
,再检验函数在![]() 时,
时,![]() 取得极小值,可得实数a的值;
取得极小值,可得实数a的值;
(Ⅱ)若函数![]() 不存在零点,则函数的值恒大于或小于0,分类讨论a,利用函数的单调性,求得函数的最值,列出不等式,可得满足条件的实数a的取值范围.
不存在零点,则函数的值恒大于或小于0,分类讨论a,利用函数的单调性,求得函数的最值,列出不等式,可得满足条件的实数a的取值范围.
解:(I)函数![]() 且
且![]() ,
,
其的定义域为R,
![]() ,
,
因为函数![]() 在
在![]() 处取得极值,
处取得极值,
所以![]() 即
即![]() ,
,
经检验,当![]() 时,
时,![]() 取得极小值,
取得极小值,
故![]() ;
;
(Ⅱ)![]() ,由于
,由于![]() ,
,
(i)当![]() 时,
时,![]() 恒成立,
恒成立,
则![]() 是增函数,
是增函数,
且当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]()
解得![]() ,
,
取![]() ,则
,则![]() ,
,
所以函数![]() 存在零点,
存在零点,
(ii)当![]() 时,由
时,由![]() =0,得
=0,得![]() ,
,
在![]() 上,
上,![]() ,
,![]() 单调递减,
单调递减,
在![]() 上,
上,![]() ,
,![]() 单调递增,
单调递增,
所以![]() 时,
时,![]() 取得最小值,
取得最小值,
函数![]() 不存在零点,等价于
不存在零点,等价于![]() ,
,
即![]() ,
,
解得![]() ,
,
综上所述:所求的实数a的取值范围是![]() .
.

【题目】为了了解一个智力游戏是否与性别有关,从某地区抽取男女游戏玩家各200请客,其中游戏水平分为高级和非高级两种.
(1)根据题意完善下列![]() 列联表,并根据列联表判断是否有99%以上的把握认为智力游戏水平高低与性别有关?
列联表,并根据列联表判断是否有99%以上的把握认为智力游戏水平高低与性别有关?
性别 | 高级 | 非高级 | 合计 |
女 | 40 | ||
男 | 140 | ||
合计 |
(2)按照性别用分层抽样的方法从这些人中抽取10人,从这10人中抽取3人作为游戏参赛选手;
![]() 若甲入选了10人名单,求甲成为参赛选手的概率;
若甲入选了10人名单,求甲成为参赛选手的概率;
![]() 设抽取的3名选手中女生的人数为
设抽取的3名选手中女生的人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
附表: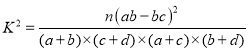 ,其中
,其中![]() .
.
| 0.010 | 0.05 | 0.001 |
| 6.635 | 7.879 | 10.828 |
【题目】2019年国际篮联篮球世界杯,将于2019年在的北京、广州、南京、上海、武汉、深圳、佛山、东莞八座城市举行.为了宣传世界杯,某大学从全校学生中随机抽取了![]() 名学生,对是否收看篮球世界杯赛事的情况进行了问卷调查,统计数据如下:
名学生,对是否收看篮球世界杯赛事的情况进行了问卷调查,统计数据如下:
会收看 | 不会收看 | |
男生 | 60 | 20 |
女生 | 20 | 20 |
(1)根据上表说明,能否有![]() 的把握认为收看篮球世界杯赛事与性别有关?
的把握认为收看篮球世界杯赛事与性别有关?
(2)现从参与问卷调查且收看篮球世界杯赛事的学生中,采用按性别分层抽样的方法选取![]() 人参加2019年国际篮联篮球世界杯赛志愿者宣传活动.
人参加2019年国际篮联篮球世界杯赛志愿者宣传活动.
(i)求男、女学生各选取多少人;
(ii)若从这![]() 人中随机选取
人中随机选取![]() 人到校广播站开展2019年国际篮联篮球世界杯赛宣传介绍,求恰好选到
人到校广播站开展2019年国际篮联篮球世界杯赛宣传介绍,求恰好选到![]() 名男生的概率.
名男生的概率.
附: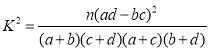 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
【题目】2019年国际篮联篮球世界杯将于2019年8月31日至9月15日在中国的北京、广州、南京、上海、武汉、深圳、佛山、东莞八座城市举行.为了宣传国际篮联篮球世界杯,某大学从全校学生中随机抽取了120名学生,对是否会收看该国际篮联篮球世界杯赛事的情况进行了问卷调查,统计数据如下:
会收看 | 不会收看 | |
男生 | 60 | 20 |
女生 | 20 | 20 |
(1)根据上表说明,能否有99%的把握认为是否会收看该国际篮联篮球世界杯赛事与性别有关?
(2)甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为![]() 与
与![]() ,且乙投球3次均未命中的概率为
,且乙投球3次均未命中的概率为![]() .
.
(i)求乙投球的命中率![]() ;
;
(ii)若甲投球1次,乙投球2次,两人共命中的次数记为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附: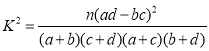 ,其中
,其中![]() ,
,
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
【题目】3月底,我国新冠肺炎疫情得到有效防控,但海外确诊病例却持续暴增,防疫物资供不应求,某医疗器械厂开足马力,日夜生产防疫所需物品.已知该厂有两条不同生产线![]() 和
和![]() 生产同一种产品各10万件,为保证质量,现从各自生产的产品中分别随机抽取20件,进行品质鉴定,鉴定成绩的茎叶图如下所示:
生产同一种产品各10万件,为保证质量,现从各自生产的产品中分别随机抽取20件,进行品质鉴定,鉴定成绩的茎叶图如下所示:
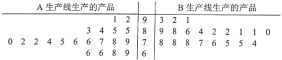
该产品的质量评价标准规定:鉴定成绩达到![]() 的产品,质量等级为优秀;鉴定成绩达到
的产品,质量等级为优秀;鉴定成绩达到![]() 的产品,质量等级为良好;鉴定成绩达到
的产品,质量等级为良好;鉴定成绩达到![]() 的产品,质量等级为合格.将这组数据的频率视为整批产品的概率.
的产品,质量等级为合格.将这组数据的频率视为整批产品的概率.
(1)从等级为优秀的样本中随机抽取两件,记![]() 为来自
为来自![]() 机器生产的产品数量,写出
机器生产的产品数量,写出![]() 的分布列,并求
的分布列,并求![]() 的数学期望;
的数学期望;
(2)请完成下面质量等级与生产线产品列联表,并判断能不能在误差不超过0.05的情况下,认为产品等级是否达到良好以上与生产产品的生产线有关.
|
| 合计 | |
良好以上 | |||
合格 | |||
合计 |
附: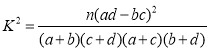
| 0.10 | 0.05 | 0.01 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
【题目】为了解高中生作文成绩与课外阅读量之间的关系,某研究机构随机抽取了100名高中生,根据问卷调查,得到以下数据:
作文成绩优秀 | 作文成绩一般 | 总计 | |
课外阅读量较大 | 35 | 20 | 55 |
课外阅读量一般 | 15 | 30 | 45 |
总计 | 50 | 50 | 100 |
(1)根据列联表,能否有99.5%的把握认为课外阅读量的大小与作文成绩优秀有关;
(2)若用分层抽样的方式从课外阅读量一般的高中生中选取了6名高中生,再从这6名高中生中随机选取2名进行面谈,求面谈的高中生中至少有1名作文成绩优秀的概率.
附: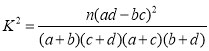 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】端午节(每年农历五月初五),是中国传统节日,有吃粽子的习俗.某超市在端午节这一天,每售出![]() kg粽子获利润
kg粽子获利润![]() 元,未售出的粽子每
元,未售出的粽子每![]() kg亏损
kg亏损![]() 元.根据历史资料,得到销售情况与市场需求量的频率分布表,如下表所示.该超市为今年的端午节预购进了
元.根据历史资料,得到销售情况与市场需求量的频率分布表,如下表所示.该超市为今年的端午节预购进了![]() kg粽子.以
kg粽子.以![]() (单位:kg,
(单位:kg,![]() )表示今年的市场需求量,
)表示今年的市场需求量,![]() (单位:元)表示今年的利润.
(单位:元)表示今年的利润.
市场需求量(kg) |
|
|
|
|
|
频率 | 0.1 | 0.2 | 0.3 | 0.25 | 0.15 |
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)在频率分布表的市场需求量分组中,以各组的区间中间值代表该组的各个值,需求量落入该区间的频率作为需求量取该区间中间值的概率(例如:若需求量![]() ,则取
,则取![]() ,且
,且![]() 的概率等于需求量落入
的概率等于需求量落入![]() 的频率
的频率![]() ),求
),求![]() 的数学期望.
的数学期望.