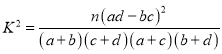题目内容
【题目】2019年国际篮联篮球世界杯将于2019年8月31日至9月15日在中国的北京、广州、南京、上海、武汉、深圳、佛山、东莞八座城市举行.为了宣传国际篮联篮球世界杯,某大学从全校学生中随机抽取了120名学生,对是否会收看该国际篮联篮球世界杯赛事的情况进行了问卷调查,统计数据如下:
会收看 | 不会收看 | |
男生 | 60 | 20 |
女生 | 20 | 20 |
(1)根据上表说明,能否有99%的把握认为是否会收看该国际篮联篮球世界杯赛事与性别有关?
(2)甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为![]() 与
与![]() ,且乙投球3次均未命中的概率为
,且乙投球3次均未命中的概率为![]() .
.
(i)求乙投球的命中率![]() ;
;
(ii)若甲投球1次,乙投球2次,两人共命中的次数记为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附: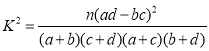 ,其中
,其中![]() ,
,
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
【答案】(1)有99%的把握认为是否会收看该国际篮联篮球世界杯赛事与性别有关;(2)(i)![]() ;(ii)分布列见解析,
;(ii)分布列见解析,![]()
【解析】
(1)由数据求得![]() ,进而与6.635比较大小即可;
,进而与6.635比较大小即可;
(2)(i)根据二项分布的概率公式求解即可;
(ii)![]() 可取0,1,2,3,利用二项分布及独立事件的概率公式求得概率,即可得到分布列与期望.
可取0,1,2,3,利用二项分布及独立事件的概率公式求得概率,即可得到分布列与期望.
(1)由表中数据可得![]() 的观测值
的观测值![]() ,
,
所以有99%的把握认为是否会收看该国际篮联篮球世界杯赛事与性别有关.
(2)(i)![]() (乙投球3次均未命中)
(乙投球3次均未命中)![]() ,
,![]() ,解得
,解得![]() .
.
(ii)![]() 可取0,1,2,3,
可取0,1,2,3,
则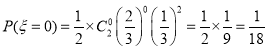 ,
,
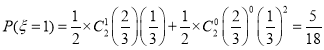 ,
,
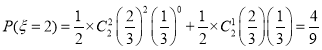 ,
,
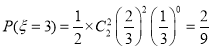 ,
,
∴![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
∴![]() .
.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目