题目内容
8.已知函数$f(x)=\frac{{{2^x}-1}}{{{2^x}+1}}$.(1)判断函数f(x)的奇偶性;
(2)用函数单调性定义证明f(x)在(-∞,+∞)上是增函数,并求出f(x)的值域.
分析 (1)直接利用奇函数的定义判断函数为定义域上的奇函数;
(2)利用函数的单调性定义证明函数为(-∞,+∞)上的增函数,再把函数解析式变形求得函数值域.
解答 (1)解:∵$f(x)=\frac{{{2^x}-1}}{{{2^x}+1}}$的定义域为R,且f(-x)=$\frac{{2}^{-x}-1}{{2}^{-x}+1}$=$\frac{\frac{1-{2}^{x}}{{2}^{x}}}{\frac{1+{2}^{x}}{{2}^{x}}}$=$-\frac{{2}^{x}-1}{{2}^{x}+1}$=-f(x),
∴f(x)是奇函数;
(2)证明:设x1,x2∈(-∞,+∞),且x1<x2,
则f(x1)-f(x2)=$\frac{{2}^{{x}_{1}}-1}{{2}^{{x}_{1}}+1}-\frac{{2}^{{x}_{2}}-1}{{2}^{{x}_{2}}+1}$=$\frac{{2}^{{x}_{1}+{x}_{2}}+{2}^{{x}_{1}}-{2}^{{x}_{2}}-1-{2}^{{x}_{1}+{x}_{2}}-{2}^{{x}_{2}}+{2}^{{x}_{1}}+1}{({2}^{{x}_{1}}+1)({2}^{{x}_{2}}+1)}$
=$\frac{2({2}^{{x}_{1}}-{2}^{{x}_{2}})}{({2}^{{x}_{1}}+1)({2}^{{x}_{2}}+1)}$.
∵x1<x2,∴${2}^{{x}_{1}}-{2}^{{x}_{2}}<0$,则$\frac{2({2}^{{x}_{1}}-{2}^{{x}_{2}})}{({2}^{{x}_{1}}+1)({2}^{{x}_{2}}+1)}$<0.
∴f(x1)<f(x2).
故f(x)在(-∞,+∞)上是增函数.
由$f(x)=\frac{{{2^x}-1}}{{{2^x}+1}}$=$\frac{{2}^{x}+1-2}{{2}^{x}+1}=1-\frac{2}{{2}^{x}+1}$,且2x+1>1,∴-2$<-\frac{2}{{2}^{x}+1}<0$,
则f(x)∈(-1,1).
即f(x)的值域为(-1,1).
点评 本题考查函数的定义域及其求法,考查了利用定义证明函数的单调性,训练了函数值域的求法,是中档题.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案| A. | {1} | B. | {1,2,4} | C. | {-1,1,2,4} | D. | {2,4} |
| A. | 1 | B. | $\frac{11}{6}$ | C. | 2 | D. | $\frac{13}{6}$ |
| A. | x3>y3 | B. | x2>y2 | C. | ln(x2+1)>ln(y2+1) | D. | $\frac{1}{{x}^{2}+1}$>$\frac{1}{{y}^{2}+1}$ |
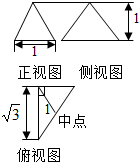 某几何体的三视图如图所示,则它的外接球的体积为( )
某几何体的三视图如图所示,则它的外接球的体积为( )| A. | 4π | B. | $\frac{8}{3}π$ | C. | $\frac{4}{9}π$ | D. | $\frac{4}{3}π$ |
| A. | -2 | B. | {2} | C. | {-2} | D. | 2∈A |