题目内容
3.已知O为△ABC的外心,$AB=2AC=2,\overrightarrow{AB}•\overrightarrow{AC}=-1$,若$\overrightarrow{AO}={x_1}\overrightarrow{AB}+{x_2}\overrightarrow{AC}$,则x1+x2的值为( )| A. | 1 | B. | $\frac{11}{6}$ | C. | 2 | D. | $\frac{13}{6}$ |
分析 如图所示,过点O分别作OD⊥AB,OE⊥AC,垂足分别为D,E.则$\overrightarrow{AO}•\overrightarrow{AB}$=$\frac{1}{2}{\overrightarrow{AB}}^{2}$=2,$\overrightarrow{AO}•\overrightarrow{AC}$=$\frac{1}{2}{\overrightarrow{AC}}^{2}$=$\frac{1}{2}$.由$\overrightarrow{AO}={x_1}\overrightarrow{AB}+{x_2}\overrightarrow{AC}$,两边分别作数量积运算即可得出.
解答  解:如图所示,
解:如图所示,
过点O分别作OD⊥AB,OE⊥AC,垂足分别为D,E.
则$\overrightarrow{AO}•\overrightarrow{AB}$=$\frac{1}{2}{\overrightarrow{AB}}^{2}$=2,$\overrightarrow{AO}•\overrightarrow{AC}$=$\frac{1}{2}{\overrightarrow{AC}}^{2}$=$\frac{1}{2}$.
∵$\overrightarrow{AO}={x_1}\overrightarrow{AB}+{x_2}\overrightarrow{AC}$,
∴$2={x}_{1}{\overrightarrow{AB}}^{2}$+${x}_{2}\overrightarrow{AB}•\overrightarrow{AC}$,$\frac{1}{2}$=${x}_{1}\overrightarrow{AB}•\overrightarrow{AC}$+${x}_{2}{\overrightarrow{AC}}^{2}$,$\overrightarrow{AB}•\overrightarrow{AC}$=-1,
化为4x1-x2=2,-x1+x2=$\frac{1}{2}$,
解得x1=$\frac{5}{6}$,x2=$\frac{4}{3}$.
∴x1+x2=$\frac{13}{6}$.
故选:D.
点评 本题考查了数量积运算性质、圆的垂经定理、三角形外心性质,考查了推理能力与计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 12 | B. | 9 | C. | 6 | D. | 3 |
| A. | $y=\frac{x^2}{x}$与y=x | B. | $y=\sqrt{x^2}$与y=x | C. | y=x0与y=1 | D. | $y=\root{3}{x^3}$与y=x |
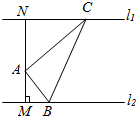 如图,A是两条平行直线之间的一定点,且点A到两平行直线的距离分别为AM=1,AN=$\sqrt{2}$,设△ABC,AC⊥AB,且顶点B、C分别在两平行直线上运动,则
如图,A是两条平行直线之间的一定点,且点A到两平行直线的距离分别为AM=1,AN=$\sqrt{2}$,设△ABC,AC⊥AB,且顶点B、C分别在两平行直线上运动,则