题目内容
【题目】如图，四棱锥
中，
，
，
为
的中点．
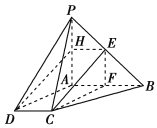
（1）求证：
平面
；
（2）在线段
上是否存在一点
，使得平面
平面
？若存在，证明你的结论，若不存在，请说明理由．
【答案】（1）证明见解析 （2）存在
的中点
满足要求，证明见解析
【解析】
（1）取
的中点
，连接
，
，证明四边形
是平行四边形，即可证明
平面
．
（2）取的中点，连接
，
，证明四边形
为平行四边形，可得
．又
平面，所以
平面，结合（1），即可证明平面
平面
．
（1）证明：取的中点，连接，，
因为
为
的中点，所以
，
，
又
，
．所以
，
，
因此四边形是平行四边形，所以
，
又
平面，
平面，
所以
平面．
（2）取的中点，连接，，所以
，
又，所以
，
又
，所以四边形为平行四边形，
所以
，
又
平面，所以
平面，
由（1）可知平面，
又
，故平面
平面，
故存在的中点满足要求．
练习册系列答案
相关题目
【题目】经销商第一年购买某工厂商品的单价为
（单位：元），在下一年购买时，购买单价与其上年度销售额（单位：万元）相联系，销售额越多，得到的优惠力度越大，具体情况如下表：
上一年度 销售额/万元 |
|
|
|
|
|
|
商品单价/元 |
|
|
|
|
|
|
为了研究该商品购买单价的情况，为此调查并整理了
个经销商一年的销售额，得到下面的柱状图.
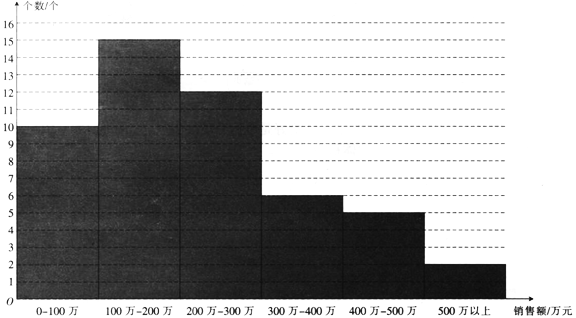
已知某经销商下一年购买该商品的单价为
（单位：元），且以经销商在各段销售额的频率作为概率.
（1）求的平均估计值.
（2）为了鼓励经销商提高销售额，计划确定一个合理的年度销售额
（单位：万元），年销售额超过的可以获得红包奖励，该工厂希望使
的经销商获得红包，估计的值，并说明理由.
