题目内容
12.若$x+m=\sqrt{1-{x^2}}$ 恰有一个实数根,则实数m的取值范围是[-1,1)∪{$\sqrt{2}$}.分析 作函数y=x+m与函数y=$\sqrt{1-{x}^{2}}$的图象,结合图象确定相切位置即可.
解答 解:作函数y=x+m与函数y=$\sqrt{1-{x}^{2}}$的图象如下,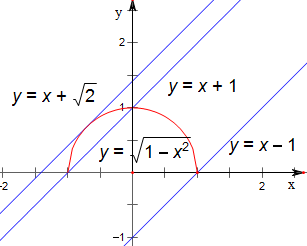
结合图象可知,
直线y=x+$\sqrt{2}$与半圆y=$\sqrt{1-{x}^{2}}$相切,
直线y=x+1与半圆y=$\sqrt{1-{x}^{2}}$有两个交点,
直线y=x-1与半圆y=$\sqrt{1-{x}^{2}}$有一个交点,
故实数m的取值范围是[-1,1)∪{$\sqrt{2}$};
故答案为:[-1,1)∪{$\sqrt{2}$}.
点评 本题考查了学生对圆与直线与函数的关系的理解与掌握,同时考查了数形结合的思想应用,属于中档题.

练习册系列答案
相关题目
1.已知|$\overrightarrow{a}$|=2,$\overrightarrow{b}$为单位向量,$\overrightarrow{a}•\overrightarrow{b}$=1,则向量$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影是( )
| A. | -$\frac{1}{2}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | -1 |
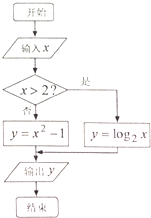 某函数的解析式由如图所示的程序框图给出.
某函数的解析式由如图所示的程序框图给出.