题目内容
【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量(单位:克)分别在[100,150),[150,200),[200,250),[250,300),[300,350),[350,400]中,经统计得频率分布直方图如图所示.
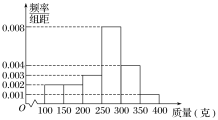
(1)现按分层抽样的方法从质量为[250,300),[300,350)内的芒果中随机抽取6个,再从这6个中随机抽取3个,求这3个芒果中恰有1个在[300,350)内的概率;
(2)某经销商来收购芒果,以各组数据的中间数代表这组数据的平均值,用样本估计总体,该种植园中还未摘下的芒果大约还有10 000个,经销商提出如下两种收购方案:A方案:所有芒果以10元/千克收购;B方案:对质量低于250克的芒果以2元/个收购,高于或等于250克的以3元/个收购.通过计算确定种植园选择哪种方案获利更多?
【答案】(1)![]() ;(2)B方案
;(2)B方案
【解析】
(1)利用枚举法求出所有可能的情况,再利用古典概型概率公式求解即可.
(2)分别计算两种方案的获利再比较大小即可.
(1)设质量在[250,300)内的4个芒果分别为A,B,C,D,质量在[300,350)内的2个芒果分别为a,b.从这6个芒果中选出3个的情况共有(A,B,C),(A,B,D),(A,B,a),(A,B,b),(A,C,D),(A,C,a),(A,C,b),(A,D,a),(A,D,b),(A,a,b),(B,C,D),(B,C,a),(B,C,b),(B,D,a),(B,D,b),(B,a,b),(C,D,a),(C,D,b),(C,a,b),(D,a,b),共计20种.其中恰有1个在[300,350)内的情况有(A,B,a),(A,B,b),(A,C,a),(A,C,b),(A,D,a),(A,D,b),(B,C,a),(B,C,b),(B,D,a),(B,D,b),(C,D,a),(C,D,b),共计12种,
因此概率P=![]() =
=![]() .
.
(2)方案A:
(125×0.002+175×0.002+225×0.003 +275×0.008+325×0.004+375×0.001) ×50×10 000×10×0.001=25 750(元).
方案B:
由题意得低于250克:
(0.002+0.002+0.003)×50×10 000×2=7 000(元);
高于或等于250克:
(0.008+0.004+0.001)×50×10 000×3=19 500(元),
所以共获利7 000+19 500=26 500(元).
由于25 750<26 500,
故B方案获利更多,应选B方案.