题目内容
【题目】已知以点 ![]() 为圆心的圆与直线
为圆心的圆与直线 ![]() 相切,过点
相切,过点 ![]() 的动直线与圆
的动直线与圆 ![]() 相交于
相交于 ![]() 两点.
两点.
(1)求圆 ![]() 的方程;
的方程;
(2)当 ![]() 时,求直线
时,求直线 ![]() 的方程.
的方程.
【答案】
(1)解: ![]() ;(2)
;(2) ![]() 或
或 ![]() . 试题
. 试题
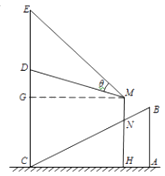
(2)解:设线段 ![]() 的中点为
的中点为 ![]() ,连结
,连结 ![]() ,则由垂径定理可知
,则由垂径定理可知 ![]() ,且
,且 ![]() ,在
,在 ![]() 中由勾股定理易知
中由勾股定理易知 ![]()
当动直线 ![]() 的斜率不存在时,直线
的斜率不存在时,直线 ![]() 的方程为
的方程为 ![]() 时,显然满足题意;
时,显然满足题意;
当动直线 ![]() 的斜率存在时,设动直线
的斜率存在时,设动直线 ![]() 的方程为:
的方程为: ![]()
由 ![]() 到动直线
到动直线 ![]() 的距离为1得
的距离为1得 ![]()
![]()
![]() 或
或 ![]() 为所求方程.
为所求方程.
【解析】(1)利用圆心到直线的距离公式求出圆的半径,从而求出圆的方程。(2)根据相交弦长的公式求出圆心到直线的距离,设出直线的方程再利用点到直线的距离公式求出直线的方程。
【考点精析】根据题目的已知条件,利用点到直线的距离公式的相关知识可以得到问题的答案,需要掌握点![]() 到直线
到直线![]() 的距离为:
的距离为: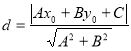 .
.

 计算高手系列答案
计算高手系列答案【题目】葫芦岛市某高中进行一项调查:2012年至2016年本校学生人均年求学花销 ![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号 | 1 | 2 | 3 | 4 | 5 |
年求学花销 | 3.2 | 3.5 | 3.8 | 4.6 | 4.9 |
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
(1)求 ![]() 关于
关于 ![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,分析2012年至2016年本校学生人均年求学花销的变化情况,并预测该地区2017年本校学生人均年求学花销情况.
【题目】某单位实行休年假制度三年以来,50名职工休年假的次数进行的调查统计结果如表所示:
根据下表信息解答以下问题:
休假次数 | 0 | 1 | 2 | 3 |
人数 | 5 | 10 | 20 | 15 |
(1)从该单位任选两名职工,用η表示这两人休年假次数之和,记“函数f(x)=x2﹣ηx﹣1在区间(4,6)上有且只有一个零点”为事件A,求事件A发生的概率P;
(2)从该单位任选两名职工,用ξ表示这两人休年假次数之差的绝对值,求随机变量ξ的分布列及数学期望Eξ.