圆内接四边形ABCD中.AB=3.BC=4.CD=5.AD=6.则cosA等于( )A．$\frac{1}{6}$B．$\frac{1}{12}$C．$\frac{1}{19}$D．$\frac{1}{21}$ 题目和参考答案——青夏教育精英家教网—

题目内容

5．圆内接四边形ABCD中，AB=3，BC=4，CD=5，AD=6，则cosA等于（　　）

A．

$\frac{1}{6}$

B．

$\frac{1}{12}$

C．

$\frac{1}{19}$

D．

$\frac{1}{21}$

分析连接BD，利用余弦定理求出cosA，cosC的关系，结合圆内接四边形的对角互补，运用诱导公式求解cosA的值．

解答解：如图，连接BD，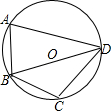
由余弦定理得，BD²=9+36-2×3×6cosA=45-36cosA，
又BD²=16+25-2×4×5cosC=41-40cosC，
∵A+C=180°，∴cosC=-cosA，
∴45-36cosA=41+40cosA，解得cosA=$\frac{1}{19}$．
故选：C．

点评本题主要考查了余弦定理，以及圆内接四边形的性质：对角互补，同时考查了运算求解的能力，属于中档题．

练习册系列答案

相关题目

19．

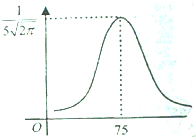某市高二理科学生数学考试的成绩x服从正态分布，其密度函数为f（x）=$\frac{1}{\sqrt{2π}σ}$e${\;}^{\frac{（x-μ）^{2}}{2{σ}^{2}}}$，密度曲线如图，已知该市理科学生总数是10000人，则成绩位于（65，85]的人数约是9544．

20．已知函数f（x）=2$\sqrt{3}$cos（$\frac{π}{2}$-x）cosx-sin²x+cos²x（x∈R）．
（1）求函数f（x）的最小正周期及单调递增区间；
（2）若f（x₀）=$\frac{6}{5}$，x₀∈[$\frac{π}{4}$，$\frac{π}{2}$]，求cos2x₀的值．

17．已知向量$\overrightarrow{a}$和$\overrightarrow{b}$的夹角为120°，且$\overrightarrow{m}$=$\frac{2\overrightarrow{a}}{|\overrightarrow{a}|}$+$\frac{\overrightarrow{b}}{|\overrightarrow{b}|}$，$\overrightarrow{n}$=-$\frac{3\overrightarrow{a}}{|\overrightarrow{a}|}$+$\frac{2\overrightarrow{b}}{|\overrightarrow{b}|}$，求$\overrightarrow{m}$与$\overrightarrow{n}$夹角的余弦值．

4．已知函数f（x）=$\frac{{e}^{x}+b}{a{e}^{x}+1}$是定义在R上的奇函数．
（1）求实数a，b的值；
（2）求函数f（x）的值域．

10．己知直线L过定点A（0，3），且与圆C：（x-3）²+（x+3）²=9相切，求该直线L的方程．

17．已知$\frac{sinα}{sinβ}$=3，$\frac{cosα}{cosβ}$=$\frac{1}{2}$，则$\frac{sin2α}{sin2β}$+$\frac{cos2α}{cos2β}$的值等于$\frac{49}{58}$．

14．已知tanθ=2，则$\frac{sinθ}{si{n}^{3}θ+co{s}^{3}θ}$=（　　）

15．2$\sqrt{5}$是数列$\sqrt{2}$，$\sqrt{5}$，2$\sqrt{2}$，$\sqrt{11}$，…的第（　　）项．

试题分类