题目内容
4.已知函数f(x)=$\frac{{e}^{x}+b}{a{e}^{x}+1}$是定义在R上的奇函数.(1)求实数a,b的值;
(2)求函数f(x)的值域.
分析 (1)利用奇函数的定义得出即$\frac{{e}^{-x}+b}{a{e}^{-x}+1}$=-$\frac{{e}^{x}+b}{a{e}^{x}+1}$,化简得出$\frac{b{e}^{x}+1}{{e}^{x}+a}$=-$\frac{{e}^{x}+b}{a{e}^{x}+1}$,即可求解a,b
(2)根据解析式得出ex=$\frac{y-1}{y+1}$>0,求解不等式即可.
解答 解:(1)∵函数f(x)=$\frac{{e}^{x}+b}{a{e}^{x}+1}$是定义在R上的奇函数.
∴f(0)=0,
即f(0)=$\frac{1+b}{a+1}$=0,∴b=-1,
又f(-x)=-f(x),即$\frac{{e}^{-x}+b}{a{e}^{-x}+1}$=-$\frac{{e}^{x}+b}{a{e}^{x}+1}$,化简得出$\frac{b{e}^{x}+1}{{e}^{x}+a}$=-$\frac{{e}^{x}+b}{a{e}^{x}+1}$,
∵b=-1,∴a=1,
(2)f(x)=$\frac{1+{e}^{x}}{1-{e}^{x}}$,
∵y=$\frac{1+{e}^{x}}{1-{e}^{x}}$,∴ex=$\frac{y-1}{y+1}$>0,
y>1或y<-1
∴函数f(x)的值域:(1,+∞)∪(-∞,-1)
点评 本题综合考查了函数的性质,运用求解值域问题,考查了学生的分析问题,运算能力,属于中档题.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
12.设随机变量ξ的分布列为P(ξ=k)=${C}_{n}^{k}$($\frac{2}{3}$)k($\frac{1}{3}$)n-k,k=0,1,2,…,n,且Eξ=24,则Dξ的值为( )
| A. | 8 | B. | 12 | C. | $\frac{2}{9}$ | D. | 16 |
5.圆内接四边形ABCD中,AB=3,BC=4,CD=5,AD=6,则cosA等于( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{19}$ | D. | $\frac{1}{21}$ |
10.集合A={y|y=2x,x∈R},B={-1,0,1},则下列结论正确的是( )
| A. | A∪B=(0,+∞) | B. | (∁RA)∪B=(-∞,0] | C. | (∁RA)∩B={-1,0} | D. | (∁RA)∩B={1} |
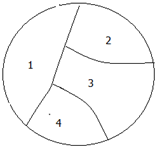 用五种不同的颜色给图中的四个区域涂色,每个区域涂一种颜色.
用五种不同的颜色给图中的四个区域涂色,每个区域涂一种颜色.