��Ŀ����
����Ŀ��Ϊ�˴����������ס��ҡ������������������Ͼ�����ϰ���ֱ��ɳ�һ�Ҿ���A��B��C.��ϰҪ���κ�ʱ�̾���A��B��C��������ͬһ��ֱ����.
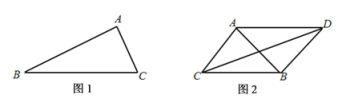
��1����ͼ1������ϰ�����У�A��B��ľ���ʼ�ձ���![]() ��B��C��ľ���ʼ�ձ���
��B��C��ľ���ʼ�ձ���![]() ����
����![]() �����ֵ.
�����ֵ.
��2����ͼ2������ϰ�����У�A��C��ľ���ʼ�ձ���![]() ��B��C��ľ���ʼ�ձ���
��B��C��ľ���ʼ�ձ���![]() .�ҵ�
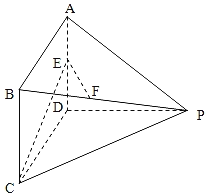
.�ҵ�![]() �仯ʱ��ģ�⺣����Dʼ�ձ��֣���B�ľ�����A��B��ľ�����ȣ�
�仯ʱ��ģ�⺣����Dʼ�ձ��֣���B�ľ�����A��B��ľ�����ȣ�![]() ����C��ֱ��AB�����࣬��C��D���������.
����C��ֱ��AB�����࣬��C��D���������.
���𰸡���1��![]() ��2��C��D���������Ϊ
��2��C��D���������Ϊ![]()
��������
��1�������Ҷ������![]() ��ȡֵ��Χ��ɵ�
��ȡֵ��Χ��ɵ�![]() �����ֵ��
�����ֵ��
��2������CΪ����ԭ�㣬CB����ֱ��Ϊx�ᣬ������ͼ��ʾ��ƽ��ֱ������ϵxOy��
��![]() ����
����![]() ����A��Բ
����A��Բ![]() ��.��
��.��![]() ����
����![]() ���ɵ�
���ɵ�![]() ��
��![]() ����C��ֱ��AB�����࣬��
����C��ֱ��AB�����࣬��![]() ���Ӷ���
���Ӷ���![]() �����꣬����
�����꣬����![]() ��켣���̿ɵ�
��켣���̿ɵ�![]() ��켣���̣�֪�켣ΪԲ���Ӷ��ɵ���Բ��λ�ù�ϵ�ɵ������룮
��켣���̣�֪�켣ΪԲ���Ӷ��ɵ���Բ��λ�ù�ϵ�ɵ������룮
��Ϊ�κ�ʱ�̾���A��B��C��������ͬһ��ֱ���ϣ����Թ���![]() ���ǽ�A��B��C�ĶԱ߷ֱ�Ϊa��b��c.
���ǽ�A��B��C�ĶԱ߷ֱ�Ϊa��b��c.
��1����![]() ��
��![]() ��
��![]() ��
��
�����Ҷ���![]() ����
����![]()
����![]() .
.
����Ϊ![]() .����
.����![]()
�𣺡�ACB�����ֵ��![]() .
.
��2����CΪ����ԭ�㣬CB����ֱ��Ϊx�ᣬ������ͼ��ʾ��ƽ��ֱ������ϵxOy��
��![]()

��Ϊ![]() ������A��Բ
������A��Բ![]() ��.
��.
��![]() ����
����![]() .
.
��ΪDʼ�ձ��֣���B�ľ�����A��B��ľ�����ȣ�
��![]() ����C��ֱ��AB�����࣬
����C��ֱ��AB�����࣬
����![]() ������
������![]() .
.
���뷽��![]() �У���
����![]() ��
��
����D���Ե�![]() ΪԲ��1Ϊ�뾶��Բ�ϣ�
ΪԲ��1Ϊ�뾶��Բ�ϣ�
��![]() .
.
��C��D���������Ϊ![]() .
.