Question

【题目】已知函数，且的最小值为．

（1）求实数的值及函数的单调递减区间；

（2）当时，若函数有且仅有一个零点，求实数的取值范围．

Answer 1

【答案】（1）或；，；（2）或．

【解析】

（1）先根据二倍角公式及辅助角公式将函数化为（，，为常数，且，）的形式，再根据函数的最小值求实数的值，最后根据正弦函数的单调性求函数的单调递减区间；（2）将在上有仅有一个零点等价转化为时，与的图象有且仅有一个交点，然后数形结合即可求解．

（1）由题意知，

，

其中，

由的最小值为，得，

解得或，

∵，∴，

∴．

令，，解得，，

故函数的单调递减区间为，．

（2）∵在上有仅有一个零点，

∴当时，与的图象有且仅有一个交点．

当时，，

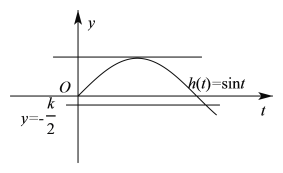
令，，，则与，的图象有且仅有一个交点，数形结合可知当或时符合要求，

即或时符合要求，

故实数的取值范围为或．