题目内容
13.设函数f(x)=$\frac{{a}^{x}-1}{1{0}^{x}+1}$(a>0且a≠1)的图象关于原点对称(1)求实数a的值,并判断f(x)的定义域内的单调性;
(2)当θ∈[0,$\frac{π}{2}$]时,有f(cos4θ+4mtanθ$\sqrt{1-si{n}^{2}θ}$)+f(-2m-2-sin4θ)<0恒成立,求实数m的取值范围.
分析 (1)根据f(x)关于原点对称便知f(x)为奇函数,从而有f(-1)=-f(1),这样即可求出a=10,从而得出$f(x)=1-\frac{2}{1{0}^{x}+1}$,根据反比例函数及指数函数、复合函数的单调性便知f(x)在R上单调递增;
(2)根据已知及f(x)的单调性、奇偶性便可由原不等式得到cos4θ+4msinθ<2m+2+sin4θ,进一步化简可得2m(1-2sinθ)>-2sin2θ-1,可考虑不等式两边同除以1-2sinθ,从而需讨论θ:$θ=\frac{π}{6}$时,不等式变成$0>-\frac{3}{2}$,显然恒成立;$0≤θ<\frac{π}{6}$时,不等式便变成$m>\frac{2si{n}^{2}θ+1}{2(2sinθ-1)}$,可换元,令sinθ=t,便得到函数y=$\frac{2{t}^{2}+1}{2(2t-1)}$,通过求导,根据导数符号可判断该函数在$[0,\frac{1}{2}),(\frac{1}{2},1]$上单调递减,从而可求出y的最大值为$y=-\frac{1}{2}$,从而得出m$>-\frac{1}{2}$;$\frac{π}{6}<θ≤\frac{π}{2}$时,根据上一步便可得出m$<\frac{3}{2}$,这几个m的范围求交集即可得出实数m的取值范围.
解答 解:(1)根据条件知,f(x)为奇函数;
∴f(-1)=-f(1);
∴$\frac{{a}^{-1}-1}{1{0}^{-1}+1}=-\frac{a-1}{10+1}$;
解得a=10,或a=1(舍去);
∴$f(x)=\frac{1{0}^{x}-1}{1{0}^{x}+1}$=$1-\frac{2}{1{0}^{x}+1}$;
可以看出x增大时,10x增大,$-\frac{2}{1{0}^{x}+1}$增大,即f(x)增大;
∴f(x)在定义域上是增函数;
(2)根据$θ∈[0,\frac{π}{2}]$及f(x)为奇函数,由原不等式得,f(cos4θ+4msinθ)<f(2m+2+sin4θ);
f(x)在R上为增函数;
∴cos4θ+4msinθ<2m+2+sin4θ;
∴(cos2θ+sin2θ)(cos2θ-sin2θ)<2m(1-2sinθ)+2;
∴2m(1-2sinθ)>-2sin2θ-1;
①若$θ=\frac{π}{6}$,则sin$θ=\frac{1}{2}$,∴$0>-\frac{1}{2}-1$恒成立;
②若$0≤θ<\frac{π}{6}$,则1-2sinθ>0;
∴$m>\frac{2si{n}^{2}θ+1}{2(2sinθ-1)}$,设sinθ=t,0≤t$<\frac{1}{2}$,则$y=\frac{2{t}^{2}+1}{2(2t-1)}$,$y′=\frac{2{t}^{2}-2t-1}{2(2t-1)^{2}}$;
令y′=0得,$t=\frac{1±\sqrt{3}}{2}$;
∴函数y在[0,$\frac{1}{2}$),($\frac{1}{2},1$]上单调递减;
∴t=0时,y在t∈[0,$\frac{1}{2}$)上取最大值$-\frac{1}{2}$;
即$\frac{2si{n}^{2}θ+1}{2(2sinθ-1)}$的最大值为$-\frac{1}{2}$;
∴$m>-\frac{1}{2}$;
③若$\frac{π}{6}<θ≤\frac{π}{2}$,则1-2sinθ<0;
∴m$<\frac{2si{n}^{2}θ+1}{2(2sinθ-1)}$;
根据上面知,sinθ=1时,$\frac{2si{n}^{2}θ+1}{2(2sinθ-1)}$取最小值$\frac{3}{2}$;
∴$m<\frac{3}{2}$;
综上得实数m的取值范围为$(-\frac{1}{2},\frac{3}{2})$.
点评 考查奇函数的定义,指数函数、反比例函数,以及复合函数的单调性,分离常数法的运用,切化弦公式,根据导数符号判断函数单调性的方法,根据单调性定义求函数的最值,要正确求导.

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案| A. | 充分但不必要条件 | B. | 必要但不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
| A. | 6 | B. | 12 | C. | 42 | D. | 90 |
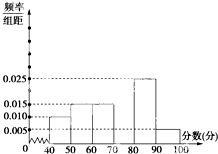 某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如下部分频率分布直方图.观察图形给出的信息,回答下列问题:
某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如下部分频率分布直方图.观察图形给出的信息,回答下列问题: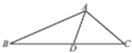 如图,在△ABC中,AB=3,AC=2,BC=4,点D在边BC上,∠BAD=30°,则sin∠CAD的值为$\frac{3\sqrt{5}+1}{8}$.
如图,在△ABC中,AB=3,AC=2,BC=4,点D在边BC上,∠BAD=30°,则sin∠CAD的值为$\frac{3\sqrt{5}+1}{8}$.