题目内容
2.已知半圆C:x2+y2=1(y≥0),A,B分别为半圆C与x轴的左右交点,直线m过点B且与x轴垂直,T是圆弧$\widehat{AB}$上的一个三等分点,连接AF并延长至直线m于S,则四边形OBST的面积为$\frac{7\sqrt{3}}{4}$或$\frac{5\sqrt{3}}{12}$.分析 由题意,∠SAB=60°或∠SAB=30°.再分类讨论,即可求出四边形OBST的面积.
解答 解:由题意,∠SAB=60°或∠SAB=30°.
∠SAB=60°,直线AT的方程为y=$\sqrt{3}$(x+1),x=1,y=2$\sqrt{3}$,
∴四边形OBST的面积为$\frac{1}{2}×2×2\sqrt{3}$-$\frac{\sqrt{3}}{4}×{1}^{2}$=$\frac{7\sqrt{3}}{4}$;
∠SAB=30°,直线AT的方程为y=$\frac{\sqrt{3}}{3}$(x+1),x=1,y=$\frac{2\sqrt{3}}{3}$,
∴四边形OBST的面积为$\frac{1}{2}×2×\frac{2\sqrt{3}}{3}-\frac{1}{2}×1×1×\frac{\sqrt{3}}{2}$=$\frac{5\sqrt{3}}{12}$.
故答案为:$\frac{7\sqrt{3}}{4}$或$\frac{5\sqrt{3}}{12}$.
点评 本题考查四边形OBST的面积,考查分类讨论的数学思想,考查学生的计算能力,属于中档题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
12.已知集合A={x|-1≤x≤1},B={x|x>0},则A∩(∁RB)=( )
| A. | {x|-1≤x≤0} | B. | {x|-1≤x<0} | C. | {x|-1≤x≤1} | D. | {x|x≤1} |
7.任取两个满足1≤m<n≤3的实数m,n,则椭圆mx2+ny2=1的离心率小于$\frac{\sqrt{2}}{2}$的概率为( )
| A. | $\frac{15}{16}$ | B. | $\frac{1}{16}$ | C. | $\frac{7}{8}$ | D. | $\frac{1}{8}$ |
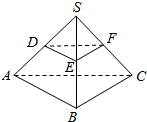 如图所示,正三棱锥S-ABC中,D,E,F分别是棱SA,SB,SC上的点,且SD=a,平面DEF∥底面ABC,且三棱台DEF-ABC与三棱锥S-ABC的所有棱长之和相等,则三棱锥S-DEF的外接球的表面积为$\frac{3π}{2}$a2.
如图所示,正三棱锥S-ABC中,D,E,F分别是棱SA,SB,SC上的点,且SD=a,平面DEF∥底面ABC,且三棱台DEF-ABC与三棱锥S-ABC的所有棱长之和相等,则三棱锥S-DEF的外接球的表面积为$\frac{3π}{2}$a2.