题目内容
14.已知M为椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1上一动点,过M作椭圆的切线为l,过椭圆的右焦点F1作l的垂线,垂足为D,求D点的轨迹方程为x2+y2=25.分析 当切线l的斜率存在且不为0时,设l的方程为y=kx+m,与椭圆方程联立得(9+25k2)x2+50kmx+25m2-225=0,根据直线l和椭圆E有且仅有一个交点,可得△=0,25k2+9.由于直线MD与l垂直,可得直线MD的方程,与l联立,消去m,k即可得出D点的轨迹方程.
解答 解:(i)当切线l的斜率存在且不为0时,设l的方程为y=kx+m①,
联立直线与椭圆方程,消去y并整理,得(9+25k2)x2+50kmx+25m2-225=0,
∵直线l和椭圆E有且仅有一个交点,∴△=2500k2m2-4(9+25k2)(25m2-225)=0,
化简并整理,得m2=25k2+9.
∵直线MD与l垂直,∴直线MD的方程为:y=-$\frac{1}{k}$(x-4)②,
联立①②,解得x=$\frac{4-km}{1+{k}^{2}}$,y=$\frac{4k+m}{1+{k}^{2}}$,
∴x2+y2=($\frac{4-km}{1+{k}^{2}}$)2+($\frac{4k+m}{1+{k}^{2}}$)2=$\frac{{m}^{2}+16}{1+{k}^{2}}$=25.(*)
(ii)当切线l的斜率为0时,此时D(4,±3),符合(*)式.
(iii)当切线l的斜率不存在时,此时D(±5,0),符合(*)式.
故答案为:x2+y2=25.
点评 本题主要考查轨迹方程、直线与椭圆相切的位置关系,考查学生运算能力、推理论证以及分析问题、解决问题的能力,考查数形结合、化归与转化思想,属于中档题.

练习册系列答案
相关题目
9.已知F为抛物线y2=4x的焦点,点A,B在该抛物线上,$\overrightarrow{OA}$$•\overrightarrow{OB}$=0(其中O为坐标原点),则△ABO与△BFO面积之差的最小值是( )
| A. | 4 | B. | 8 | C. | 8$\sqrt{3}$ | D. | 16$\sqrt{3}$ |
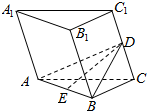 在正三棱柱ABC-A1B1C1中,E是AB的中点,D是CC1上一点.
在正三棱柱ABC-A1B1C1中,E是AB的中点,D是CC1上一点.