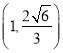题目内容
【题目】定义:对于一个项数为![]() 的数列
的数列![]() ,若存在
,若存在![]() 且
且![]() ,使得数列
,使得数列![]() 的前k项和与剩下项的和相等(若仅为1项,则和为该项本身),我们称该数列是“等和数列”.例如:因为
的前k项和与剩下项的和相等(若仅为1项,则和为该项本身),我们称该数列是“等和数列”.例如:因为![]() ,所以数列3,2,1是“等和数列”.请解答以下问题:
,所以数列3,2,1是“等和数列”.请解答以下问题:
(1)数列1,2,p,4是“等和数列”,求实数p的值;
(2)项数为![]() 的等差数列
的等差数列![]() 的前n项和为
的前n项和为![]() ,
,![]() ,求证:
,求证:![]() 是“等和数列”.
是“等和数列”.
(3)![]() 是公比为q项数为
是公比为q项数为![]() 的等比数列
的等比数列![]() ,其中
,其中![]() 且
且![]() 恒成立.判断
恒成立.判断![]() 是不是“等和数列”,并证明你的结论.
是不是“等和数列”,并证明你的结论.
【答案】(1)![]() 或
或![]() 或
或![]() (2)证明见解析 (3)
(2)证明见解析 (3)![]() 不是“等和数列”,证明见解析
不是“等和数列”,证明见解析
【解析】
(1)对令![]() 分别计算,得到答案.
分别计算,得到答案.
(2)由![]() ,得
,得![]() ,若
,若![]() 是“等和数列,存在k使得
是“等和数列,存在k使得![]() ,即
,即![]() .分
.分![]() 和
和![]() 进行讨论即可.
进行讨论即可.
(3)假设![]() 是“等和数列”, 则存在
是“等和数列”, 则存在![]() 且
且![]() ,使得
,使得![]() 成立, 即
成立, 即![]() ,
,
由![]() 会得到矛盾,从而判断处结论.
会得到矛盾,从而判断处结论.
(1)若![]() ,即
,即![]() ,则
,则![]() .
.
若![]() ,即
,即![]() ,则
,则![]() .
.
若![]() ,即
,即![]() ,则
,则![]() .
.
所以![]() 或
或![]() 或
或![]()
(2)证明方法一:![]() ,所以
,所以![]() .
.
假设存在k使得数列![]() 的前k项和与剩下项的和相等,即
的前k项和与剩下项的和相等,即![]() ,所以
,所以![]() .
.
![]() ,
,![]() ,
,
即![]() .
.
当![]() 时,
时,![]() ,对任意
,对任意![]() 都有
都有![]() ,
,![]() ,即
,即![]() ,
,
所以此时![]() 是“等和数列”;
是“等和数列”;
当![]() 时,
时,![]() ,
,![]() ,此时
,此时![]() 或
或![]() (舍去).
(舍去).
即存在![]() 且
且![]() ,使得
,使得![]() 成立,所以此时
成立,所以此时![]() 是“等和数列”.
是“等和数列”.
由上得:![]() 是“等和数列”
是“等和数列”
证明方法二:设![]() 公差为d,
公差为d,
![]() ,
,![]() ,
,
同理:![]() ,
,![]() ,
,
于是![]() ,同理
,同理![]() ,
,
![]() ,即
,即![]() ,
,![]() ,
,![]() ,
,![]() 成等差数列,
成等差数列,
所以![]() ,因为
,因为![]() ,
,
所以![]() ,即存在
,即存在![]() ,使得
,使得![]() ,所以
,所以![]() 是“等和数列”
是“等和数列”
(3)![]() 不是“等和数列”
不是“等和数列”
证明方法一:设![]() 为
为![]() 的前n项和
的前n项和
反证法:假设结论不成立,即![]() 是“等和数列”,
是“等和数列”,
则存在![]() 且
且![]() ,使得
,使得![]() 成立,即
成立,即![]() ,
,
于是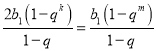 成立,即
成立,即![]()
![]() 时,
时,![]() ,
,![]() ,即
,即![]() ,所以
,所以![]() ,
,
所以![]() ,与
,与![]() 产生矛盾.所以假设不成立,即
产生矛盾.所以假设不成立,即![]() 不是“等和数列”.
不是“等和数列”.
证明方法二:反证法:假设结论不成立,即![]() 是“等和数列”,
是“等和数列”,
则存在![]() 且
且![]() ,使得
,使得![]() 成立,即
成立,即![]() .
.
于是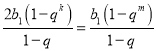 成立,即
成立,即![]() 得到
得到![]() ,
,
这里![]() ,
,![]() 得
得![]() 产生矛盾.所以假设不成立,即
产生矛盾.所以假设不成立,即![]() 不是“等和数列”.
不是“等和数列”.
证明方法三:先证该数列满足:设![]() 为
为![]() 前n项和,则对任意
前n项和,则对任意![]() 都有
都有![]() 成立.
成立.
证明: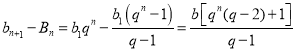 ,
,
因为![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,
,
所以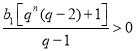 ,所以
,所以![]() 恒成立.
恒成立.
由此得:对任意![]() 且
且![]() ,
,![]() ,即
,即![]() ,
,
所以不存在![]() 且
且![]() ,使得
,使得![]() 成立,
成立,
即![]() 不是“等和数列”.
不是“等和数列”.