题目内容
已知命题p：?x∈（0，+∞），3x＞2x，命题q：?x∈（-∞，0），|x|＞2-x，则下列命题为真命题的是（ ）
| A．p∧q | B．（￢p）∧q | C．（￢p）∧（￢q） | D．p∧（￢q） |
结合指数函数的单调性，
当x∈（0，+∞）时，3x＞2x成立，
∴命题P为真命题，
对于命题q：不等式|x|＞2-x
当x∈（-∞，0）时，解得
-x＞2-x，即0＞2，显然不成立，
∴命题q为假命题，
选项A中，p∧q为假命题；
选项B中，（￢p）∧q为假命题；
选项C中，（￢p）∧（￢q）为假命题；
只有选项D为真命题，
故选D．
当x∈（0，+∞）时，3x＞2x成立，
∴命题P为真命题，
对于命题q：不等式|x|＞2-x
当x∈（-∞，0）时，解得
-x＞2-x，即0＞2，显然不成立，
∴命题q为假命题，
选项A中，p∧q为假命题；
选项B中，（￢p）∧q为假命题；
选项C中，（￢p）∧（￢q）为假命题；
只有选项D为真命题，
故选D．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
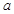=1”是“函数f(x)=
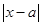在区间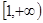
上为增函数”的 （ ）