题目内容
【题目】已知在等比数列{an}中，a1=2，且a1，a2，a3-2成等差数列．
（1）求数列{an}的通项公式；
（2）若数列{bn}满足：
，求数列{bn}的前n项和Sn．
【答案】（1）an=2n，n∈N*（2）1-
+n2
【解析】
（1）等比数列{an}的公比设为q，由等差数列中项性质和等比数列的通项公式，解方程可得q，进而得到所求通项公式；
（2）求得
=
+2log22n-1=+2n-1，由数列的分组求和和等差数列、等比数列的求和公式，计算可得所求和．
（1）等比数列{an}的公比设为q，a1=2，
a1，a2，a3-2成等差数列，可得2a2=a1+a3-2，
即为4q=2+2q2-2，解得q=2，
则an=a1qn-1=2n，n∈N*；
（2）=+2log22n-1=+2n-1，
则数列{bn}的前n项和Sn=（
+
+…+）+（1+3+…+2n-1）
=
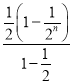+n（1+2n-1）=1-+n2．
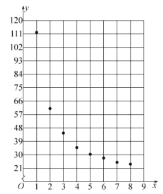
【题目】某企业新研发了一种产品，产品的成本由原料成本及非原料成本组成，每件产品的非原料成本y（元）与生产该产品的数量x（千件）有关，经统计得到如下数据：
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y | 112 | 61 | 44.5 | 35 | 30.5 | 28 | 25 | 24 |
根据以上数据，绘制了散点图．
参考数据：（其中
）
|
|
|
|
|
|
183.4 | 0.34 | 0.115 | 1.53 | 360 | 22385.8 |
参考公式：对于一组数据
，
，其回归直线
的斜率和截距的最小二乘估计分别为：
．
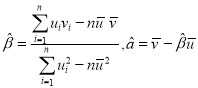（1）观察散点图判断，
与
哪一个适宜作为非原料成本y与生产该产品的数量x的回归方程类型？（给出判断即可，不必说明理由）
（2）根据（1）的判断结果及表中数据，建立y与x的回归方程．
（3）试预测生产该产品10000件时每件产品的非原料成本.
【题目】某工厂为提高生产效率，开展技术创新活动，提出了完成某项生产任务的两种新的生产方式．为比较两种生产方式的效率，选取40名工人，将他们随机分成两组，每组20人，第一组工人用第一种生产方式，第二组工人用第二种生产方式．根据工人完成生产任务的工作时间（单位：min）绘制了如下茎叶图：
（1）根据茎叶图判断哪种生产方式的效率更高？并说明理由；
（2）求40名工人完成生产任务所需时间的中位数
，并将完成生产任务所需时间超过和不超过的工人数填入下面的列联表：
超过 | 不超过 | |
第一种生产方式 | ||
第二种生产方式 |
（3）根据（2）中的列联表，能否有99%的把握认为两种生产方式的效率有差异？
附：
，
|
|
|
|
|
|
|
|
