题目内容
17.已知f(x)满足f(1+$\frac{1}{x}$)=$\frac{1}{x}$+$\frac{{x}^{2}+1}{{x}^{2}}$,求f(x)的解析式.分析 把解析式配方得出f(1$+\frac{1}{x}$)=($\frac{1}{x}$+1)2-($\frac{1}{x}$+1)+1,整体换元即可求解.
解答 解:∵f(1+$\frac{1}{x}$)=$\frac{1}{x}$+$\frac{{x}^{2}+1}{{x}^{2}}$,
∴f(1$+\frac{1}{x}$)=($\frac{1}{x}$+1)2-($\frac{1}{x}$+1)+1,
设t=1$+\frac{1}{x}$,f(t)=t2-t+1,
∵1$+\frac{1}{x}$≠1
∴f(x)=x2-x+1,x≠1.
点评 本题考察了运用配方法,换元法求解函数的解析式,关键是注意变量的范围限制,属于中档题.

练习册系列答案
相关题目
9.已知{an}是等比数列,有a3•a11=4a7,{bn}是等差数列,且a7=b7,则b5+b9=( )
| A. | 4 | B. | 8 | C. | 0或8 | D. | 16 |
6.直线y=kx+b与曲线y=x3-3x+1相切于点(2,3),则b的值为( )
| A. | -3 | B. | 9 | C. | -7 | D. | -15 |
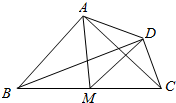 如图,四边形ABCD满足$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\overrightarrow{DB}$•$\overrightarrow{DC}$=0,|$\overrightarrow{AB}$|=2|$\overrightarrow{DC}$|=2,若M是BC的中点,则$\overrightarrow{AB}$•$\overrightarrow{AM}$-$\overrightarrow{DM}$•$\overrightarrow{DC}$=( )
如图,四边形ABCD满足$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\overrightarrow{DB}$•$\overrightarrow{DC}$=0,|$\overrightarrow{AB}$|=2|$\overrightarrow{DC}$|=2,若M是BC的中点,则$\overrightarrow{AB}$•$\overrightarrow{AM}$-$\overrightarrow{DM}$•$\overrightarrow{DC}$=( )