题目内容
5. 如图,阴影部分(包括边界)为平面区域D,若点P(x,y)在区域D内,则z=x+2y的最小值是-1;x,y满足的约束条件是$\left\{\begin{array}{l}2x-y+2≥0\\ x≤0\\ y≥0.\end{array}\right.$.
如图,阴影部分(包括边界)为平面区域D,若点P(x,y)在区域D内,则z=x+2y的最小值是-1;x,y满足的约束条件是$\left\{\begin{array}{l}2x-y+2≥0\\ x≤0\\ y≥0.\end{array}\right.$.
分析 化目标函数为直线方程斜截式,由可行域得到最优解,把最优解的坐标代入目标函数求得目标函数的最小值,直接由可行域得到约束条件.
解答 解:如图,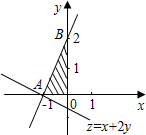
化目标函数z=x+2y为$y=-\frac{x}{2}+\frac{z}{2}$,
由图可知,当直线$y=-\frac{x}{2}+\frac{z}{2}$过A(-1,0)时直线在y轴上的截距最小,
z有最小值为-1.
由图可知,满足可行域的约束条件为$\left\{\begin{array}{l}2x-y+2≥0\\ x≤0\\ y≥0.\end{array}\right.$.
故答案为:-1,$\left\{\begin{array}{l}2x-y+2≥0\\ x≤0\\ y≥0.\end{array}\right.$.
点评 本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
20.已知a>b>0,那么下列不等式成立的是( )
| A. | 2b-2a>0 | B. | b2-a2>0 | C. | |b|>|a| | D. | 2a>2b |
10.我国法律规定,公民同时具备以下条件才能享有选举权:(一)享有政治权利;(二)年满18周岁;(三)具有中华人民共和国国籍;(四)无精神病.由此可知,“年满10周岁”是“享有选举权”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
17.若实数x,y满足约束条件$\left\{\begin{array}{l}1≤x+y≤3\\-1≤x-y≤1\end{array}\right.$,则z=2x+y的取值范围是( )
| A. | [0,6] | B. | [1,6] | C. | [1,5] | D. | [0,5] |
14.一个随机变量ξ的概率分布律如下:
其中A,B,C为锐角三角形ABC的三个内角.
(1)求A的值;
(2)若x1=cosB,x2=sinC,求数学期望Eξ的取值范围.
| ξ | x1 | x2 |
| P | cos2A | sin(B+C) |
(1)求A的值;
(2)若x1=cosB,x2=sinC,求数学期望Eξ的取值范围.
15.“直线(m+2)x+3my+1=0与“直线(m-2)x+(m+2)y-3=0相互垂直”是“m=$\frac{1}{2}$”的( )
| A. | 充分必要条件 | B. | 充分而不必要条件 | ||
| C. | .必要而不充分条件 | D. | 既不充分也不必要条件 |