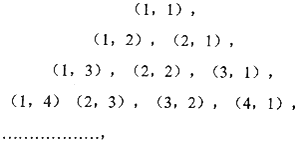题目内容
【题目】求证： 
﹣ 
＜ 
﹣ 
（a≥3）．
【答案】证明：欲证 
﹣ 
＜ 
﹣ 
，
只需证：（ 
）2＜（ 
）2 ， 即2a﹣2﹣2 
＜2a﹣4﹣2 
．
只需证： ＞1+ ，
只需证：a2﹣2a＞a2﹣4a+4+2 ，即a﹣2＞ ，
只需证：a2﹣4a+4＞a2﹣4a+3，
只需证：4＞3．
显然，4＞3恒成立，
∴ ﹣ ＜ ﹣ （a≥3）
【解析】使用分析法逐步找出使不等式成立的条件即可．
【考点精析】本题主要考查了不等式的证明的相关知识点，需要掌握不等式证明的几种常用方法:常用方法有：比较法（作差，作商法）、综合法、分析法；其它方法有：换元法、反证法、放缩法、构造法，函数单调性法，数学归纳法等才能正确解答此题．
练习册系列答案
相关题目
【题目】设连续掷两次骰子得到的点数分别为m、n，令平面向量 
， 
．
（1）求使得事件“ 
”发生的概率；
（2）求使得事件“ 
”发生的概率；
（3）使得事件“直线 
与圆（x﹣3）2+y2=1相交”发生的概率．
【题目】PM2.5是指空气中直径小于或等于2.5微米的颗粒物（也称可入肺颗粒物）．为了探究车流量与PM2.5的浓度是否相关，现采集到某城市周一至周五某一时间段车流量与PM2.5的数据如表：
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量x（万辆） | 50 | 51 | 54 | 57 | 58 |
PM2.5的浓度y（微克/立方米） | 69 | 70 | 74 | 78 | 79 |
（1）根据上表数据，请在如图坐标系中画出散点图； 
（2）根据上表数据，用最小二乘法求出y关于x的线性回归方程 
；（保留2位小数）
（3）若周六同一时间段车流量是25万辆，试根据（2）求出的线性回归方程预测，此时PM2.5的浓度为多少（保留整数）？
参考公式： 
= 
， 
= 
﹣ 
．
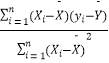