题目内容
【题目】已知椭圆C: ![]() =1(a>b>0)的右焦点为F2(1,0),点P(1,
=1(a>b>0)的右焦点为F2(1,0),点P(1, ![]() )在椭圆C上.
)在椭圆C上.
(1)求椭圆C的方程;
(2)过坐标原点O的两条直线EF,MN分别与椭圆C交于E,F,M,N四点,且直线OE,OM的斜率之积为﹣ ![]() ,求证:四边形EMFN的面积为定值.
,求证:四边形EMFN的面积为定值.
【答案】
(1)解:∵为点 ![]() 在椭圆C上,椭圆C的右焦点为F2(1,0),
在椭圆C上,椭圆C的右焦点为F2(1,0),
则 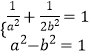 ,解得
,解得 ![]() ,
,
∴椭圆C的方程为 ![]() .
.
(2)解:当直线EM斜率存在时,设直线方程为l:y=kx+m,E(x1,y1),M(x2,y2),
联立 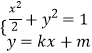 得(1+2k2)x2+4kmx+2m2﹣2=0,
得(1+2k2)x2+4kmx+2m2﹣2=0, 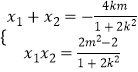 ,
,
![]() =
= ![]() ,
,
由 ![]()
![]() 得
得 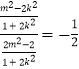 ,即2m2=2k2+1,
,即2m2=2k2+1,
原点到直线EM的距离为 ![]() ,
,
∴ ![]()
= ![]() =
= ![]()
= ![]()
= ![]() ,
,
∴ ![]() .
.
当直线EM斜率不存在时, ![]() ,x1=x2,y1=﹣y2,∴
,x1=x2,y1=﹣y2,∴ ![]() ,
,
又 ![]() ,解得
,解得 ![]() ,
, ![]() ,
, ![]() .
.
【解析】(1)由题意可得: 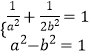 ,解出即可得出.(2)当直线EM斜率存在时,设直线方程为l:y=kx+m,E(x1 , y1),M(x2 , y2),与椭圆方程联立得(1+2k2)x2+4kmx+2m2﹣2=0,利用斜率计算公式、根与系数的关系及其
,解出即可得出.(2)当直线EM斜率存在时,设直线方程为l:y=kx+m,E(x1 , y1),M(x2 , y2),与椭圆方程联立得(1+2k2)x2+4kmx+2m2﹣2=0,利用斜率计算公式、根与系数的关系及其 ![]() ,可得2m2=2k2+1,原点到直线EM的距离为
,可得2m2=2k2+1,原点到直线EM的距离为 ![]() ,利用
,利用 ![]() ,代入化简即可得出定值,斜率不存在时也成立.
,代入化简即可得出定值,斜率不存在时也成立.

【题目】设连续掷两次骰子得到的点数分别为m、n,令平面向量 ![]() ,
, ![]() .
.
(1)求使得事件“ ![]() ”发生的概率;
”发生的概率;
(2)求使得事件“ ![]() ”发生的概率;
”发生的概率;
(3)使得事件“直线 ![]() 与圆(x﹣3)2+y2=1相交”发生的概率.
与圆(x﹣3)2+y2=1相交”发生的概率.
【题目】如表中给出了2011年~2015年某市快递业务总量的统计数据(单位:百万件)
年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
快递业务总量 | 34 | 55 | 71 | 85 | 105 |
(1)在图中画出所给数据的折线图; 
(2)建立一个该市快递量y关于年份代码x的线性回归模型;
(3)利用(2)所得的模型,预测该市2016年的快递业务总量.
附:回归直线方程的斜率和截距的最小二乘估计公式分别为:
斜率: 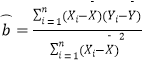 ,纵截距:
,纵截距: ![]() .
.