题目内容
【题目】已知函数f(x)=|2x﹣a|+|x﹣a+1|.
(1)当a=4时,求解不等式f(x)≥8;
(2)已知关于x的不等式f(x)![]() 在R上恒成立,求参数a的取值范围.
在R上恒成立,求参数a的取值范围.
【答案】(1)[5,+∞)∪(∞,![]() ];(2)[﹣2,1].
];(2)[﹣2,1].
【解析】
(1)根据a=4时,有f(x)=|2x﹣4|+|x﹣3|,然后利用绝对值的几何意义,去绝对值求解.
(2)根据绝对值的零点有a﹣1和![]() ,分a﹣1
,分a﹣1![]() ,a﹣1
,a﹣1![]() 和a﹣1
和a﹣1![]() 时三种情况分类讨论求解.
时三种情况分类讨论求解.
(1)当a=4时,f(x)=|2x﹣4|+|x﹣3|,
(i)当x≥3时,原不等式可化为3x﹣7≥8,解可得x≥5,
此时不等式的解集[5,+∞);
(ii)当2<x<3时,原不等式可化为2x﹣4+3﹣x≥8,解可得x≥9
此时不等式的解集;
(iii)当x≤2时,原不等式可化为﹣3x+7≥8,解可得x![]() ,
,
此时不等式的解集(∞,![]() ],
],
综上可得,不等式的解集[5,+∞)∪(∞,![]() ],
],
(2)(i)当a﹣1![]() 即a=2时,f(x)=3|x﹣1|
即a=2时,f(x)=3|x﹣1|![]() 2显然不恒成立,
2显然不恒成立,
(ii)当a﹣1![]() 即a>2时,
即a>2时,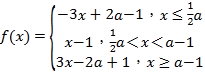 ,
,
结合函数的单调性可知,当x![]() 时,函数取得最小值f(
时,函数取得最小值f(![]() )
)![]() ,
,
若f(x)![]() 在R上恒成立,则
在R上恒成立,则![]() ,此时a不存在,
,此时a不存在,
(iii)当a﹣1![]() 即a<2时,f(x)
即a<2时,f(x)
若f(x)![]() 在R上恒成立,则1
在R上恒成立,则1![]() ,
,
解得﹣2≤a≤1,
此时a的范围[﹣2,1],
综上可得,a的范围围[﹣2,1].

 名校课堂系列答案
名校课堂系列答案【题目】某家庭记录了未使用节水龙头50天的日用水量数据(单位:m3)和使用了节水龙头50天的日用水量数据,得到频数分布表如下:
未使用节水龙头50天的日用水量频数分布表
日用 水量 |
|
|
|
|
|
|
|
频数 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
使用了节水龙头50天的日用水量频数分布表
日用 水量 |
|
|
|
|
|
|
频数 | 1 | 5 | 13 | 10 | 16 | 5 |
(1)在答题卡上作出使用了节水龙头50天的日用水量数据的频率分布直方图:
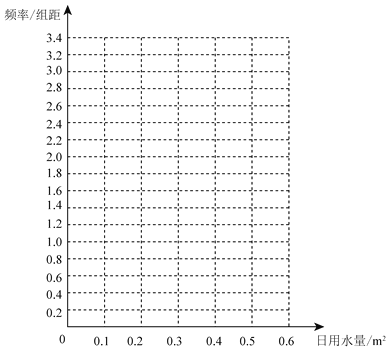
(2)估计该家庭使用节水龙头后,日用水量小于0.35 m3的概率;
(3)估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表.)