题目内容
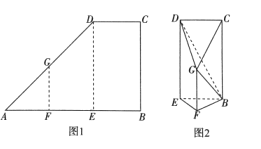
【题目】如图,正四棱锥![]() 的底边长为2,侧棱长为
的底边长为2,侧棱长为![]() ,
,![]() 为
为![]() 上一点,且
上一点,且![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 上的点,且
上的点,且![]() .
.
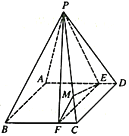
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求锐二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)由正方形的性质知![]() ,又由相似三角形可得
,又由相似三角形可得![]() ,
,
再结合面面平行的判定定理即可证明;
(2)由已知条件可推导出![]() ,
,![]() ,
,![]() 两两垂直,建立空间直角坐标系,
两两垂直,建立空间直角坐标系,
求出平面的法向量,利用公式即可求锐二面角的余弦值.
(1)![]()
![]() ,且
,且![]() ,
,
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,
![]()
![]() ,又
,又![]() 平面
平面![]() ,
,
![]()
![]() 平面
平面![]() ,
,
![]()
![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,![]()
![]() ,又
,又![]() 平面
平面![]() ,
,
![]()
![]() 平面
平面![]() ,
,
![]()
![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ;
;
(2)如图,连接![]() ,
,![]() 相交于点
相交于点![]() ,连接
,连接![]() ,
,
![]() 四棱锥
四棱锥![]() 为正四棱锥,
为正四棱锥,
![]()
![]() ,
,![]() ,
,
又![]() ,∴
,∴![]() ,且
,且![]() ,
,
同理可得![]() ,∴
,∴![]() ,
,![]() ,
,![]() 两两垂直,
两两垂直,
故建立如图所示的空间直角坐标系,
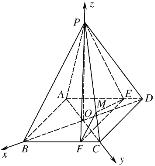
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
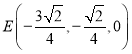 ,
, ,
,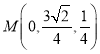 ,
,![]() ,
,
![]()
![]() ,
,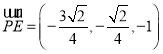 ,
,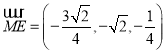 ,
,
令平面![]() 的法向量为
的法向量为![]() ,
,
则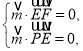 即
即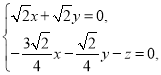
解得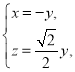
![]() 取
取![]() ,则
,则![]() ,
,![]() ,
,
故![]() ,
,
同理可得平面![]() 的一个法向量
的一个法向量![]() ,
,
∴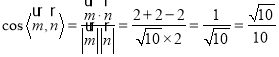 ,
,
![]() 锐二面角
锐二面角![]() 的余弦值为
的余弦值为![]() .
.

 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案【题目】在综合素质评价的某个维度的测评中,依据评分细则,学生之间相互打分,最终将所有的数据合成一个分数,满分100分,按照大于或等于80分的为优秀,小于80分的为合格,为了解学生的在该维度的测评结果,在毕业班中随机抽出一个班的数据.该班共有60名学生,得到如下的列联表:
优秀 | 合格 | 总计 | |
男生 | 6 | ||
女生 | 18 | ||
合计 | 60 |
已知在该班随机抽取1人测评结果为优秀的概率为![]() .
.
(1)完成上面的列联表;
(2)能否在犯错误的概率不超过0.10的前提下认为性别与测评结果有关系?
(3)现在如果想了解全校学生在该维度的表现情况,采取简单随机抽样方式在全校学生中抽取少数一部分来分析,请你选择一个合适的抽样方法,并解释理由.
附: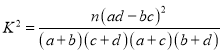
| 0.25 | 0.10 | 0.025 |
| 1.323 | 2.706 | 5.024 |
【题目】某省从2021年开始将全面推行新高考制度,新高考“![]() ”中的“2”要求考生从政治、化学、生物、地理四门中选两科,按照等级赋分计入高考成绩,等级赋分规则如下:从2021年夏季高考开始,高考政治、化学、生物、地理四门等级考试科目的考生原始成绩从高到低划分为
”中的“2”要求考生从政治、化学、生物、地理四门中选两科,按照等级赋分计入高考成绩,等级赋分规则如下:从2021年夏季高考开始,高考政治、化学、生物、地理四门等级考试科目的考生原始成绩从高到低划分为![]() 五个等级,确定各等级人数所占比例分别为
五个等级,确定各等级人数所占比例分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,等级考试科目成绩计入考生总成绩时,将
,等级考试科目成绩计入考生总成绩时,将![]() 至
至![]() 等级内的考生原始成绩,依照等比例转换法分别转换到
等级内的考生原始成绩,依照等比例转换法分别转换到![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五个分数区间,得到考生的等级分,等级转换分满分为100分.具体转换分数区间如下表:
五个分数区间,得到考生的等级分,等级转换分满分为100分.具体转换分数区间如下表:
等级 |
|
|
|
|
|
比例 |
|
|
|
|
|
赋分区间 |
|
|
|
|
|
而等比例转换法是通过公式计算:![]()
其中![]() ,
,![]() 分别表示原始分区间的最低分和最高分,
分别表示原始分区间的最低分和最高分,![]() 、
、![]() 分别表示等级分区间的最低分和最高分,
分别表示等级分区间的最低分和最高分,![]() 表示原始分,
表示原始分,![]() 表示转换分,当原始分为
表示转换分,当原始分为![]() ,
,![]() 时,等级分分别为
时,等级分分别为![]() 、
、![]()
假设小南的化学考试成绩信息如下表:
考生科目 | 考试成绩 | 成绩等级 | 原始分区间 | 等级分区间 |
化学 | 75分 |
|
|
|
设小南转换后的等级成绩为![]() ,根据公式得:
,根据公式得:![]() ,
,
所以![]() (四舍五入取整),小南最终化学成绩为77分.
(四舍五入取整),小南最终化学成绩为77分.
已知某年级学生有100人选了化学,以半期考试成绩为原始成绩转换本年级的化学等级成绩,其中化学成绩获得![]() 等级的学生原始成绩统计如下表:
等级的学生原始成绩统计如下表:
成绩 | 95 | 93 | 91 | 90 | 88 | 87 | 85 |
人数 | 1 | 2 | 3 | 2 | 3 | 2 | 2 |
(1)从化学成绩获得![]() 等级的学生中任取2名,求恰好有1名同学的等级成绩不小于96分的概率;
等级的学生中任取2名,求恰好有1名同学的等级成绩不小于96分的概率;
(2)从化学成绩获得![]() 等级的学生中任取5名,设5名学生中等级成绩不小于96分人数为
等级的学生中任取5名,设5名学生中等级成绩不小于96分人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.