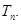题目内容
数列{an}的首项为3,{bn}为等差数列且bn=an+1-an(n∈N*).若b3=-2,b10=12,求a8的值
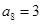
解析试题分析:先利用等差数列的通项公式分别表示出b3和b10,联立方程求得b1和d的值,进而利用叠加法求得b1+b2+…+bn=an+1-a1,最后利用等差数列的求和公式求得所求先求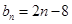 再递推或叠加求
再递推或叠加求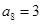
解:依题意可知b1+2d=-2,b1+9d=12,解得b1=-6,d=2,∵bn=an+1-an,∴b1+b2+…+bn=an+1-a1,,∴a8=b1+b2+…+b7+3= 。
。
考点:数列的递推式
点评:本题主要考查了数列的递推式,以及对数列基础知识的熟练掌握,同时考查了运算求解的能力,属于基础题.

练习册系列答案
相关题目
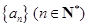 的前
的前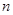 项和为
项和为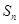 ,且
,且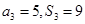 .
.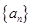 的通项公式;
的通项公式;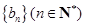 ,若
,若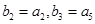 ,求数列
,求数列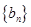 的前
的前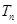 .
.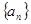 是一个等差 数列,且
是一个等差 数列,且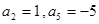 。
。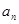 ; (2)求
; (2)求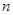 项和
项和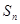 的最大值。
的最大值。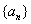 中,
中, 为前n项和,且满足
为前n项和,且满足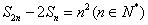
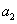 及数列
及数列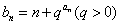 ,求数列
,求数列 的前n项和
的前n项和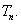
 的前n项和为
的前n项和为 ,且满足
,且满足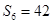 ,
,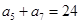 .
.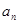 及前n项和
及前n项和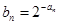 (
(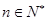 ),求数列
),求数列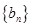 的前
的前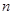 项和
项和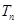 .
.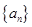 的前四项和为10,且
的前四项和为10,且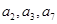 成等比数列
成等比数列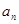
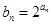 ,求数列
,求数列 的前
的前 项和
项和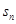
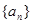 是等差数列,
是等差数列,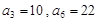 ,数列
,数列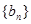 的前n项和是
的前n项和是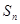 ,且
,且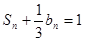 .
.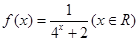 .
.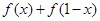 的值;
的值;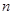 项和公式的推导方法,求:
项和公式的推导方法,求: 的值.
的值.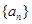 的前
的前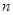 项和为
项和为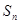 ,且
,且
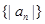 的前
的前