题目内容
(本小题满分12分)如图,圆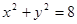 内有一点P(—1,2),AB为过点P的弦。
内有一点P(—1,2),AB为过点P的弦。
(1)当弦AB的倾斜角为135°时,求AB所在的直线方程及|AB|;
(2)当弦AB被点P平分时,写出直线AB的方程。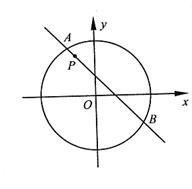
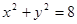 内有一点P(—1,2),AB为过点P的弦。
内有一点P(—1,2),AB为过点P的弦。(1)当弦AB的倾斜角为135°时,求AB所在的直线方程及|AB|;
(2)当弦AB被点P平分时,写出直线AB的方程。

(1)x+y-1=0 |AB|=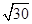 (2)x-2y+5=0
(2)x-2y+5=0
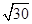 (2)x-2y+5=0
(2)x-2y+5=0(1)由倾斜角可得斜率为-1,然后根据过点P,写成点斜式,然后化成一般式即可。先求出圆心到直线AB的距离d,然后根据|AB|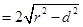 求值即可。
求值即可。
(2)根据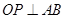 可求出AB的斜率,然后根据过点P,写出点斜式,转化为一般式方程即可。
可求出AB的斜率,然后根据过点P,写出点斜式,转化为一般式方程即可。
解:(1)x+y-1=0 |AB|=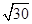 (2)x-2y+5=0
(2)x-2y+5=0
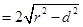 求值即可。
求值即可。(2)根据
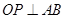 可求出AB的斜率,然后根据过点P,写出点斜式,转化为一般式方程即可。
可求出AB的斜率,然后根据过点P,写出点斜式,转化为一般式方程即可。解:(1)x+y-1=0 |AB|=
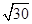 (2)x-2y+5=0
(2)x-2y+5=0
练习册系列答案
相关题目
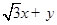 的最小值是 ( )
的最小值是 ( )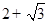
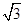
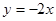 上,并且与直线
上,并且与直线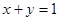 相切于点A(2,-1).
相切于点A(2,-1).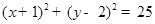 ,直线方程为
,直线方程为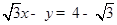 求(Ⅰ)圆心到直线的距离
求(Ⅰ)圆心到直线的距离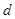 ;
;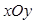 中,已知以
中,已知以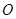 为圆心的圆与直线
为圆心的圆与直线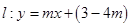
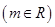 恒有公共点,且要求使圆
恒有公共点,且要求使圆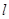 过定点,并指出定点坐标;
过定点,并指出定点坐标;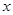 轴相交于
轴相交于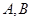 两点,圆内动点
两点,圆内动点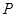 使
使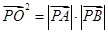 ,求
,求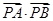 的取值范围.
的取值范围. 的距离的最大值是( )
的距离的最大值是( )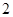
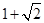


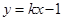 与圆
与圆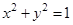 的公共点为
的公共点为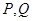 ,则
,则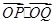 (其中
(其中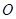 为原点)的最大值为( )
为原点)的最大值为( )



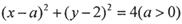 和直线
和直线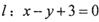 ,当直线l被圆C截得弦长为
,当直线l被圆C截得弦长为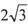 时,则a=______.
时,则a=______.