题目内容
16.若椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,点(1,$\frac{3}{2}$)在椭圆C上.(1)求椭圆C的方程;
(2)过椭圆右焦点F2 斜率为k(k≠0的直线l与椭圆C相交于E,F两点,A为椭圆的右顶点,直线AE,AF分别交直线x=3于点M,N,线段MN的中点为P,记直线PF2 的斜率为k′,求证:k•k′为定值.
分析 (1)由题意可得:$\frac{c}{a}$=$\frac{1}{2}$,$\frac{1}{{a}^{2}}$+$\frac{9}{4{b}^{2}}$=1,又a2=b2+c2,联立解得即可得出;
(2)设过椭圆右焦点F2 (1,0)斜率为k(k≠0)的直线l方程为:y=k(x-1),设点E(x1,y1),F(x2,y2),与椭圆方程联立化为(4k2+3)x2-8k2x+4k2-12=0,直线AE的方程为:$y=\frac{{y}_{1}}{{x}_{1}-2}(x-2)$,直线AF的方程为:$y=\frac{{y}_{2}}{{x}_{2}-2}(x-2)$,令x=3,可得点M,N,利用中点坐标公式可得P,可得直线PF2的斜率k′=$\frac{1}{4}$•$\frac{2k{x}_{1}{x}_{2}-3k({x}_{1}+{x}_{2})+4k}{{x}_{1}{x}_{2}-2({x}_{1}+{x}_{2})+4}$,把根与系数的关系代入即可得出.
解答 (1)解:由题意可得:$\frac{c}{a}$=$\frac{1}{2}$,$\frac{1}{{a}^{2}}$+$\frac{9}{4{b}^{2}}$=1,又a2=b2+c2,
联立解得a2=4,b2=3,c=1,
∴椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)证明:设过椭圆右焦点F2 (1,0)斜率为k(k≠0)的直线l方程为:y=k(x-1),
设点E(x1,y1),F(x2,y2),联立$\left\{\begin{array}{l}{y=k(x-1)}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,化为(4k2+3)x2-8k2x+4k2-12=0,由题意△>0,
∴${x}_{1}+{x}_{2}=\frac{8{k}^{2}}{4{k}^{2}+3}$,x1x2=$\frac{4{k}^{2}-12}{4{k}^{2}+3}$,
直线AE的方程为:$y=\frac{{y}_{1}}{{x}_{1}-2}(x-2)$,直线AF的方程为:$y=\frac{{y}_{2}}{{x}_{2}-2}(x-2)$,
令x=3,可得点M$(3,\frac{{y}_{1}}{{x}_{1}-2})$,N$(3,\frac{{y}_{2}}{{x}_{2}-2})$,
∴P$(3,\frac{1}{2}(\frac{{y}_{1}}{{x}_{1}-2}+\frac{{y}_{2}}{{x}_{2}-2}))$,
∴直线PF2的斜率k′=$\frac{\frac{1}{2}(\frac{{y}_{1}}{{x}_{1}-2}+\frac{{y}_{2}}{{x}_{2}-2})-0}{3-1}$=$\frac{1}{4}(\frac{{y}_{1}}{{x}_{1}-2}+\frac{{y}_{2}}{{x}_{2}-2})$=$\frac{1}{4}$$•\frac{{y}_{1}{x}_{2}+{y}_{2}{x}_{1}-2({y}_{1}+{y}_{2})}{{x}_{1}{x}_{2}-2({x}_{1}+{x}_{2})+4}$=$\frac{1}{4}$•$\frac{2k{x}_{1}{x}_{2}-3k({x}_{1}+{x}_{2})+4k}{{x}_{1}{x}_{2}-2({x}_{1}+{x}_{2})+4}$,
把${x}_{1}+{x}_{2}=\frac{8{k}^{2}}{4{k}^{2}+3}$,x1x2=$\frac{4{k}^{2}-12}{4{k}^{2}+3}$代入可得k′=-$\frac{3}{4k}$,
∴k′•k=-$\frac{3}{4}$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、斜率计算公式、中点坐标公式,考查了推理能力与计算能力,属于难题.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案| A. | -3 | B. | ±$\frac{1}{3}$ | C. | -$\frac{1}{3}$ | D. | -$\frac{1}{2}$ |
| A. | 48 | B. | 24 | C. | 36 | D. | 25 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 对任意x∈R,都有x2≤0 | B. | 不存在x∈R,使得x2<0 | ||
| C. | 存在x0∈R,使得x02≥0 | D. | 存在x0∈R,使得x02<0 |
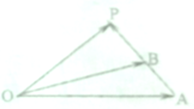 如图$\overrightarrow{OA}$,$\overrightarrow{OB}$不共线,P点在AB上,求证:存在实数λ,μ且λ+μ=1,使$\overrightarrow{OP}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$.思考:有本题你想到了什么?(用向量证明三点共线)
如图$\overrightarrow{OA}$,$\overrightarrow{OB}$不共线,P点在AB上,求证:存在实数λ,μ且λ+μ=1,使$\overrightarrow{OP}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$.思考:有本题你想到了什么?(用向量证明三点共线)