Question

【题目】已知函数，的导函数为.

（1）试讨论函数的零点个数；

（2）若对任意的，关于的不等式恒成立，求实数的取值范围.

Answer 1

【答案】（1）详见解析；（2）.

【解析】

（1）先求函数的定义域，然后求函数的导数，对分类讨论，将的零点问题，转化为直线与函数图象的交点个数来求解出来.（2）构造函数，将原问题转化为对恒成立，先利用确定的一个范围，然后利用的二阶导数验证在这个范围内，的最大值不大于零，由此求得的取值范围.

解：（1）由题意得的定义域为，.

（i）当时，，此时没有零点；

（ii）当时，，

的零点个数等于直线与函数图象的交点个数，可知直线与函数图象的相切点，此时切线的斜率为.

①当，即时，两个图象没有交点，即函数没有零点；

②当，即时，两个图象有两个交点，即函数有两个零点；

③当，即时两个图象有一个交点，即函数有一个零点；

④当，即时，两个图象有一个交点，即函数有一个零点.

综上，当时，函数没有零点；

当或时，有一个零点；

当时，有两个零点.

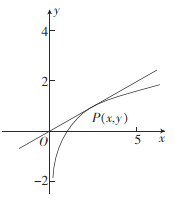
（2）设 ，

要使原不等式恒成立，则只要对恒成立，

所以.

令，则.

由于“对恒成立”的一个必要条件是，即.

当时，，，

所以在上单调递减.

所以，，从而在上单调递减，则，，

所以实数的取值范围为.