题目内容
2.已知p:“?x∈[1,3],x2-a≥0”,q:“?x∈R,x2+2ax+2-a=0”若“p∧q”是真命题,求实数a的取值范围.分析 由“p∧q”是真命题,则p为真命题,q也为真命题,若p为真命题,则a≤x2在x∈[1,3]上恒成立,解出即可.若q为真命题,即x2+2ax+2-a=0有实根,△≥0,解出,求其交集即可.
解答 解:由“p∧q”是真命题,则p为真命题,q也为真命题,
若p为真命题,则a≤x2在x∈[1,3]上恒成立,∴a≤1.
若q为真命题,即x2+2ax+2-a=0有实根,△=4a2-4(2-a)≥0,
解得a≤-2或a≥1.
综上所求实数a的取值范围为a≤-2或a=1.
点评 本题考查了复合命题真假的判定方法、恒成立问题、一元二次方程有实数根的充要条件,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
13.直线3x-$\sqrt{3}$=0的倾斜角是( )
| A. | 30° | B. | 60° | C. | 90° | D. | 不存在 |
17.f(x)=-$\frac{1}{2}$x2+bln(x+2)在(-1,+∞)上单调递减,则b的取值范围是( )
| A. | (-∞,-1) | B. | (-1,+∞) | C. | [-1,+∞) | D. | (-∞,-1] |
7.独立性检验中的统计假设就是假设相关事件A,B( )
| A. | 互斥 | B. | 不互斥 | C. | 相互独立 | D. | 不独立 |
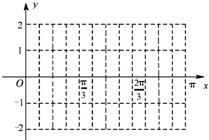 设函数f(x)=2sin(2x+φ)(0<φ<π),y=f(x)图象的一个对称中心是$(\frac{π}{3},0)$.
设函数f(x)=2sin(2x+φ)(0<φ<π),y=f(x)图象的一个对称中心是$(\frac{π}{3},0)$.