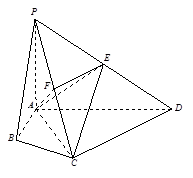题目内容
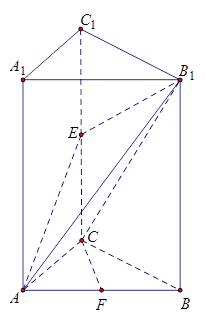
如图所示,在直三棱柱 中,
中,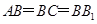 ,
, 为
为 的中点.
的中点.
(Ⅰ) 若AC1⊥平面A1BD,求证:B1C1⊥平面ABB1A1;
(Ⅱ)在(Ⅰ)的条件下,设AB=1,求三棱锥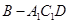 的体积.
的体积.
(I)通过证明“线线垂直”,得到“线面垂直”, ⊥面
⊥面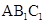 ,得到
,得到 .
.
又在直棱柱 中,
中, ,得到
,得到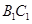 ⊥平面
⊥平面 .
.
(II)三棱锥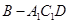 的体积
的体积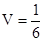 .
.
解析试题分析:(I)(I)通过证明“线线垂直”,得到“线面垂直”, ⊥面
⊥面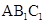 ,得到
,得到 .
.
又在直棱柱 中,
中, ,得到
,得到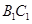 ⊥平面
⊥平面 .
.
(II)为确定三棱锥的体积,应注意明确“底面”“高”,注意遵循“一作,二证,三计算”的解题步骤.通过证明“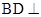 平面
平面 ”.明确
”.明确 就是三棱锥
就是三棱锥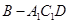 的高.
的高.
解答此类问题,容易出现的错误是忽视证明,利用直观感觉确定高.
试题解析:(I)直三棱柱 中,∵
中,∵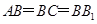 ,∴四边形
,∴四边形 为正方形,
为正方形,
∴ ,
,
又∵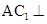 面
面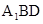 ,∴
,∴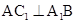 ,∴
,∴ ⊥面
⊥面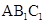 ,∴
,∴ .
.
又在直棱柱 中,
中, ,∴B1C1⊥平面ABB1A1.
,∴B1C1⊥平面ABB1A1.
(II)∵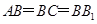 ,
, 为
为 的中点,∴
的中点,∴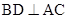 .
.
∴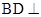 平面
平面 .
.
∴ 就是三棱锥
就是三棱锥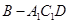 的高.
的高.
由(I)知B1C1⊥平面ABB1A1,∴ 平面ABB1A1.
平面ABB1A1.
∴ .∴
.∴ 是直角等腰三角形.
是直角等腰三角形.
又∵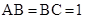 ,∴
,∴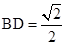 ,
,
∴ ,
,
∴三棱锥 的体积
的体积 .
.
考点:垂直关系、体积计算.

练习册系列答案
相关题目
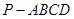 中,底面
中,底面 是边长为1的正方形,
是边长为1的正方形,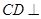 平面
平面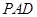 ,
, 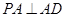 ,
,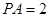 ,
,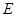 为
为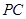 的中点,
的中点,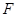 在棱
在棱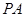 上.
上.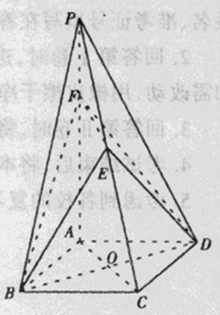
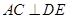 ;
;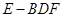 的体积.
的体积.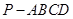 的底面是正方形,
的底面是正方形,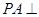 底面
底面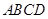 ,
,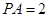 ,
, ,点
,点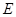 、
、 分别为棱
分别为棱 、
、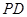 的中点.
的中点.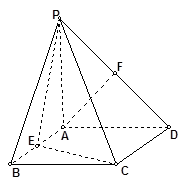
 平面
平面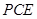 ;
;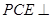 平面
平面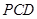 ;
;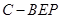 的体积.
的体积.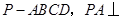 平面
平面 ,底面
,底面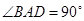 ,且
,且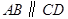 ,
,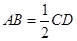 .
.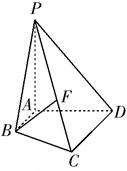
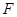 在线段
在线段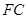 上运动,且设
上运动,且设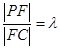 ,问当
,问当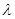 为何值时,
为何值时,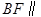 平面
平面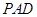 ,并证明你的结论;
,并证明你的结论;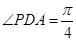 ,
,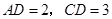 求四棱锥
求四棱锥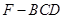 的体积.
的体积.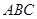 中,
中,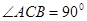 ,
,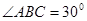 ,
,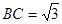 ,在三角形内挖去一个半圆(圆心
,在三角形内挖去一个半圆(圆心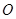 在边
在边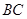 上,半圆与
上,半圆与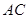 、
、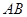 分别相切于点
分别相切于点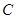 、
、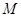 ,与
,与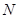 ),将△
),将△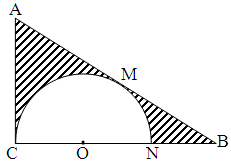
 ,AD=CD=1.
,AD=CD=1.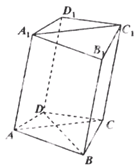
 求证:BD⊥AA1;
求证:BD⊥AA1; 若四边形
若四边形 是菱形,且
是菱形,且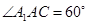 ,求四棱柱
,求四棱柱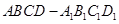 的体积.
的体积.