题目内容
设函数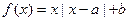
(Ⅰ) 求证: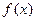 为奇函数的充要条件是
为奇函数的充要条件是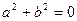 ;
;
(Ⅱ) 设常数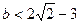 ,且对任意
,且对任意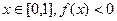 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。
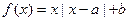
(Ⅰ) 求证:
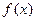 为奇函数的充要条件是
为奇函数的充要条件是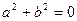 ;
;(Ⅱ) 设常数
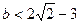 ,且对任意
,且对任意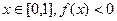 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。(Ⅰ)同解析;(Ⅱ)当
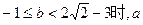 的取值范围是
的取值范围是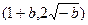 ;当
;当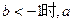 的取值范围是
的取值范围是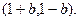
(I)充分性:若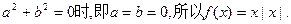
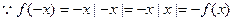 ,对一切x∈R恒成立,
,对一切x∈R恒成立,
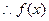 是奇函数
是奇函数
必要性:若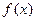 是奇函数,则对一切x∈R,
是奇函数,则对一切x∈R,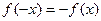 恒成立,即
恒成立,即
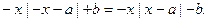
令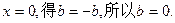
再令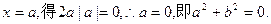
(II)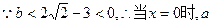 取任意实数不等式恒成立,
取任意实数不等式恒成立,
故考虑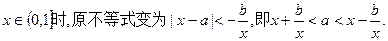
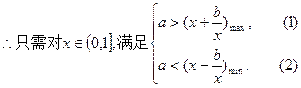
对(1)式,由b < 0时,在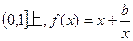 为增函数,
为增函数,
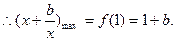
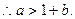 (3)
(3)
对(2)式,当
当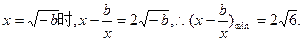
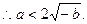 (4)
(4)
由(3)、(4),要使a存在,必须有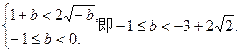
∴当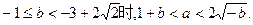
当 为减函数,(证明略)
为减函数,(证明略)
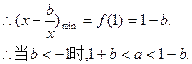
综上所述,当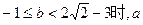 的取值范围是
的取值范围是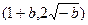 ;
;
当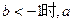 的取值范围是
的取值范围是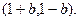
解法二: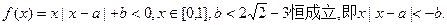
由于b是负数,故
(1)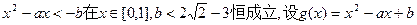 ,
,
则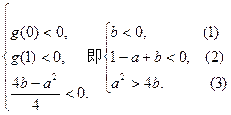
其中(1),(3)显然成立,由(2),得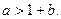 (*)
(*)
(2)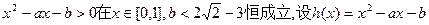 ,
,
①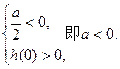
综合(*),得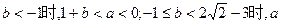 值不存在
值不存在
②
综合(*),得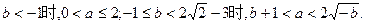
③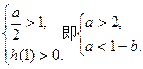
综合(*),得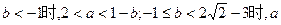 不存在
不存在
综上,得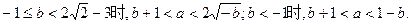
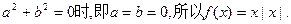
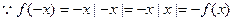 ,对一切x∈R恒成立,
,对一切x∈R恒成立,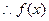 是奇函数
是奇函数必要性:若
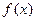 是奇函数,则对一切x∈R,
是奇函数,则对一切x∈R,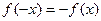 恒成立,即
恒成立,即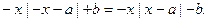
令
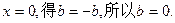
再令
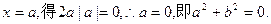
(II)
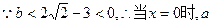 取任意实数不等式恒成立,
取任意实数不等式恒成立,故考虑
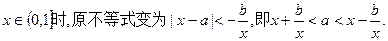
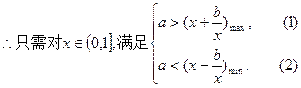
对(1)式,由b < 0时,在
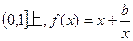 为增函数,
为增函数,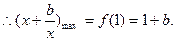
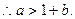 (3)
(3)对(2)式,当

当
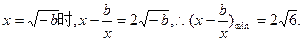
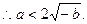 (4)
(4)由(3)、(4),要使a存在,必须有
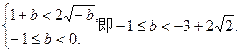
∴当
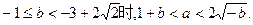
当
 为减函数,(证明略)
为减函数,(证明略)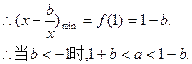
综上所述,当
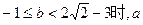 的取值范围是
的取值范围是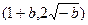 ;
;当
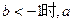 的取值范围是
的取值范围是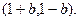
解法二:
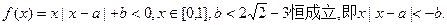
由于b是负数,故

(1)
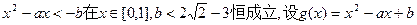 ,
,则
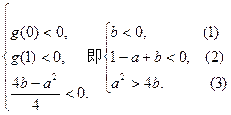
其中(1),(3)显然成立,由(2),得
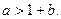 (*)
(*)(2)
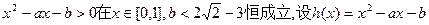 ,
,①
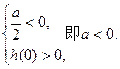
综合(*),得
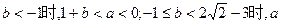 值不存在
值不存在 ②

综合(*),得
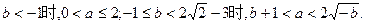
③
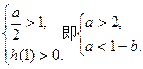
综合(*),得
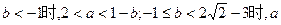 不存在
不存在 综上,得
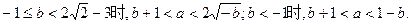

练习册系列答案
相关题目
 ,若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.如果函数f(x)=
,若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.如果函数f(x)=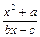 有且仅有两个不动点0和2.
有且仅有两个不动点0和2.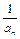 )=1,
)=1,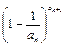 <
<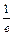 <
<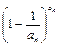 ;
;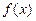 是定义在
是定义在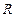 上的单调奇函数, 且
上的单调奇函数, 且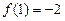 .
.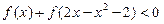 .
.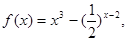 则其零点所在的区间为 ( )
则其零点所在的区间为 ( )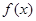 同时满足下列条件:①是奇函数;②在[0,1]上是增函数;③在
同时满足下列条件:①是奇函数;②在[0,1]上是增函数;③在 ,已知实数x,y满足|x|≤2,|y|≤2,
,已知实数x,y满足|x|≤2,|y|≤2,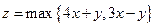 则z的取值范围是 ( )
则z的取值范围是 ( ) 上的函数
上的函数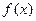 满足
满足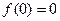 ,
,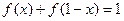 ,且
,且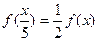 ,当
,当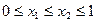 时,有
时,有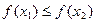 ,求
,求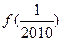 的值
的值