题目内容
已知函数 ,在
,在 时取得极值.
时取得极值.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)若 时,
时, 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(Ⅲ)若 ,是否存在实数b,使得方程
,是否存在实数b,使得方程 在区间
在区间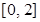 上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由.
上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由.
 ,在
,在 时取得极值.
时取得极值.(Ⅰ)求函数
 的解析式;
的解析式;(Ⅱ)若
 时,
时, 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;(Ⅲ)若
 ,是否存在实数b,使得方程
,是否存在实数b,使得方程 在区间
在区间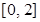 上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由.
上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由.(Ⅰ)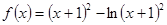 (Ⅱ)
(Ⅱ)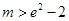 (Ⅲ)
(Ⅲ)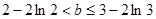
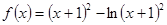 (Ⅱ)
(Ⅱ)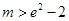 (Ⅲ)
(Ⅲ)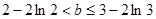
试题分析:(Ⅰ)
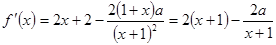 2分
2分依题意得
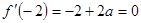 ,所以
,所以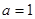 ,从而
,从而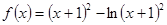 4分
4分(Ⅱ)
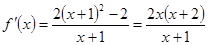 令
令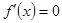 ,得
,得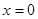 或
或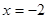 (舍去),
(舍去),当
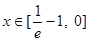 时,
时,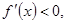 当
当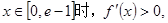
由讨论知
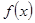 在
在 的极小值为
的极小值为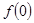 ;最大值为
;最大值为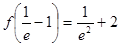 或
或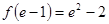 ,因为
,因为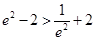 ,所以最大值为
,所以最大值为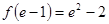 ,所以
,所以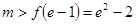 ……8分
……8分(Ⅲ)设
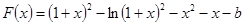 ,即
,即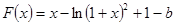 ,
,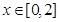 .
.又
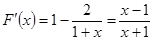 ,令
,令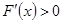 ,得
,得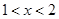 ;令
;令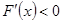 ,得
,得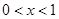 .
.所以函数
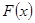 的增区间
的增区间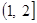 ,减区间
,减区间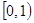 .
.要使方程有两个相异实根,则有
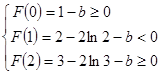 ,解得
,解得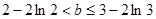 12分
12分点评:第一问利用函数在极值点处的导数为零得到系数的值,第二问第三问将不等式恒成立问题转化为求函数最值问题,进而利用函数导数求单调性求极值最值。这种转化思路在函数题目中经常用到,要加强这方面的训练

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 ;
; 的最大值;
的最大值; 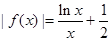 是否有实数解 .
是否有实数解 .
 ,解不等式
,解不等式 ;
; 的不等式
的不等式
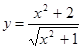 ;②
;②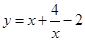 ;③
;③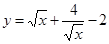 ;④
;④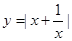 ;⑤
;⑤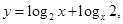 其中
其中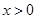 且
且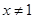 ;⑥
;⑥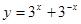 .其中最小值为2的函数是 (填入序号 ).
.其中最小值为2的函数是 (填入序号 ).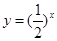 的定义域为
的定义域为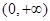 ;②函数
;②函数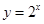 与函数
与函数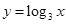 互为反函数;
互为反函数;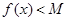 (
(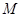 为常数),则函数
为常数),则函数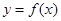 的最大值为
的最大值为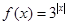 的值域为
的值域为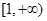 .
.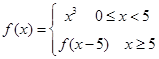 ,那么
,那么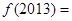 ( )
( )

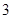
 是以
是以 为周期的偶函数,当
为周期的偶函数,当 时,
时, .若关于
.若关于 的方程
的方程 (
( )在区间
)在区间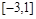 内有四个不同的实根,则
内有四个不同的实根,则 的取值范围是
的取值范围是


